Содержание:

Определения

Площадь является одним из основных математических понятий. Она характеризует как плоские, так и поверхностные геометрические объекты.

Определение

Площадью плоской замкнутой фигуры называется величина части плоскости, которая находится внутри указанной фигуры.

Единицей измерения площади плоской фигуры является квадрат со стороной, равной единице. Число, соответствующее площади некоторой фигуры, состоящей из частей, равно сумме чисел, соответствующих площадям этих частей. Измерение площадей треугольников и многоугольников основано на возможности построения равновеликих им прямоугольников.

Площадь произвольной ограниченной плоской фигуры определяется как общий предел площадей описанных и вписанных в нее многоугольников, наибольшие стороны которых по длине стремятся к нулю.

Если фигура имеет площадь, то она называется квадрируемой.

Формулы площади основных геометрических фигур

Площадь треугольника

Чтобы найти площадь треугольника, надо найти полупроизведение двух его сторон на синус угла между ними. То есть если известны длины двух сторон треугольника $ABC$, которые равны $a$ и $b$, а также угол $\alpha$ между этими сторонами, то искомая площадь:

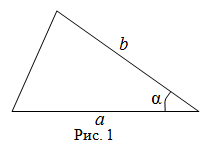
$$\mathrm{S}_{\Delta A B C}=\frac{1}{2} a b \sin \alpha$$

Читать дальше: формулы площади треугольника и примеры решений →

Площадь круга

Чтобы найти площадь круга, надо найти произведение числа $\pi$ на квадрат радиуса этого круга, то есть

$$\mathrm{S}_{\kappa p}=\pi R^{2}$$

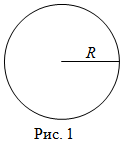
Читать дальше: формула площади круга и примеры решений →


Площадь квадрата

Чтобы найти площадь квадрата, надо длину его стороны возвести в квадрат, то есть

$$S=a^2$$

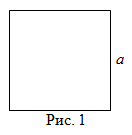
Читать дальше: формула площади квадрата и примеры решений →


Площадь прямоугольника

Чтобы найти площадь прямоугольника, надо его длину умножить на ширину, то есть

$$S=ab$$

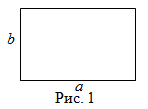
Читать дальше: формула площади прямоугольника и примеры решений →

Площадь параллелограмма

Чтобы найти площадь параллелограмма, нужно найти произведение стороны $a$ параллелограмма на высоту 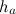, проведенную к этой стороне, то есть

$$S=ah_{a}$$

Читать дальше: формулы площади параллелограмма и примеры решений →


Площадь трапеции

Чтобы найти площадь трапеции, нужно длину средней линии 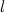умножить на длину высоты 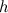, опущенной к основанию:

$$S=lh$$

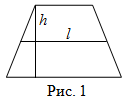
Читать дальше: формулы площади трапеции и примеры решений →


Площадь ромба

Чтобы найти площадь ромба, надо длину стороны умножить на длину высоты, проведенной к этой стороне:

$$S=ah_{a}$$

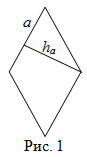
Читать дальше: формулы площади ромба и примеры решений →

Площадь эллипса

Чтобы найти площадь эллипса, нужно найти произведение длин большой и малой полуосей этого эллипса на число $\pi$, то есть

$$S=\pi ab$$

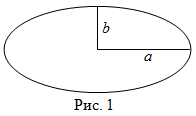
Читать дальше: формула площади эллипса и примеры решений →