Задание. Найти площадь круга, если известно, что его радиус равен 3 м.
Решение. Площадь круга вычисляется по формуле:
$$\mathrm{S}_{k p}=\pi R^{2}$$Подставляя в эту формулу значение радиуса $R=3$ м, получаем:
$\mathrm{S}_{k p}=\pi \cdot 3^{2}=9 \pi$ (м2)
Ответ. $\mathrm{S}_{k p}=9 \pi$ (м2)
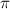 на квадрат радиуса этого круга, то есть
на квадрат радиуса этого круга, то есть