Формулы объема

Содержание:

• Формула объема куба
• Формула объема пирамиды
• Формулы объема конуса
• Формулы объема цилиндра
• Формула объема шара
• Формула объема тетраэдра

Объём геометрической фигуры - количественная характеристика пространства, занимаемого телом или веществом. В простейших случаях объём измеряется числом умещающихся в теле единичных кубов, т. е. кубов с ребром, равным единице длины. Объём тела или вместимость сосуда определяется его формой и линейными размерами.

Формула объема куба

1) Объем куба равен кубу его ребра.

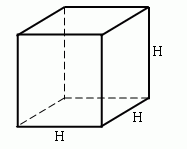
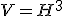
V - объем куба

H - высота ребра куба

См. также: Программа для расчета объема куба.

Формула объема пирамиды

1) Объем пирамиды равен одной трети произведения площади основания S (ABCD) на высоту h (OS).

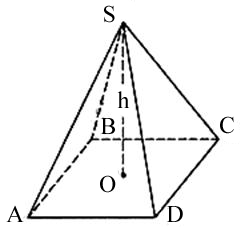
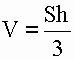
V - объем пирамиды

S - площадь основания пирамиды

h - высота пирамиды

См. также: Программа для расчета объема пирамиды.

Формулы объема конуса

1) Объем конуса равен одной трети произведения площади основания на высоту.

2) Объем конуса равен одной трети произведения числа пи (3.1415) на квадрат радиуса основания на высоту.

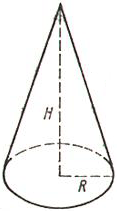
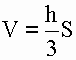
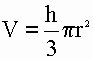
V - объем конуса

S - площадь основания конуса

h - высота конуса

π - число пи (3.1415)

r - радиус конуса

См. также: Программа для расчета объема конуса.

Формулы объема цилиндра

1) Объем цилиндра равен произведению площади основания на высоту.

2) Объем цилиндра равен произведению числа пи (3.1415) на квадрат радиуса основания на высоту.

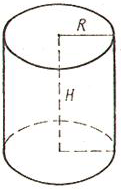
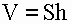
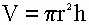
V - объем цилиндра

S - площадь основания цилиндра

h - высота цилиндра

π - число пи (3.1415)

r - радиус цилиндра

См. также: Программа для расчета объема цилиндра.

Формула объема шара

1) Объем шара вычисляется по приведенной ниже формуле.

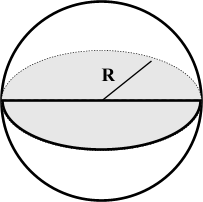
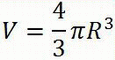
V - объем шара

π - число пи (3.1415)

R - радиус шара

См. также: Программа для расчета объема шара.

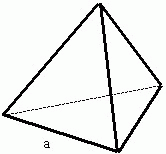
Формула объема тетраэдра

1) Объем тетраэдра равен дроби в числителе которой корень квадратный из двух помноженный на куб длины ребра тетраэдра, а в знаменателе двенадцать.

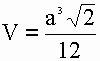
V - объем тетраэдра

a - длина ребра тетраэдра

См. также: Программа для расчета объема тетраэдра.

Warning: file_put_contents(./students_count.txt): failed to open stream: Permission denied in /var/www/webmath-q2ws/data/www/webmath.ru/poleznoe/guide_content_banner.php on line 20

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 460 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Узнать стоимость