Содержание:
- Квадрат суммы:
- Квадрат разности:
- Разность квадратов:
- Куб суммы:
- Куб разности:
- Сумма кубов:
- Разность кубов:
- Квадрат суммы:
- Квадрат разности:
- Разность квадратов:
- Куб суммы:
- Куб разности:
- Сумма кубов:
- Разность кубов:
В некоторых конкретных случаях можно умножение одного выражения (многочлена, числа) на другое (другой многочлен, число) свести к компактному, легко запоминающемуся результату. То есть на практике можно сэкономить время, не умножая каждый раз одно выражение на другое, а воспользовавшись уже известным результатом. Такие случаи называют формулами сокращенного умножения:
Выражения 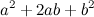 и
и
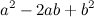 ,
стоящие в правых частях равенств (1) и (2), называются соответственно полный квадрат суммы и
полный квадрат разности.
,
стоящие в правых частях равенств (1) и (2), называются соответственно полный квадрат суммы и
полный квадрат разности.
Выражения 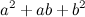 и
и
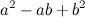 ,
которые стоят вторыми сомножителями в правых частях равенств (6), (7), называются соответственно
неполный квадрат суммы и неполный квадрат разности. От полных квадратов суммы и разности они отличаются лишь средним
коэффициентом.
,
которые стоят вторыми сомножителями в правых частях равенств (6), (7), называются соответственно
неполный квадрат суммы и неполный квадрат разности. От полных квадратов суммы и разности они отличаются лишь средним
коэффициентом.
Все формулы сокращенного умножения доказываются непосредственным раскрытием скобок и приведением подобных слагаемых.
Заметим, что любое математическое равенство "читается" в математике как слева направо, то есть левая часть равенства заменяется равной ей правой частью, так и наоборот: справа налево, то есть правая часть равенства заменяется левой. А тогда приведенные формулы сокращенного умножения можно записать и в виде:
Формулы сокращенного умножения применяются непосредственно для сокращенного умножения, для разложения выражений на множители. С их помощью можно сравнительно быстро и легко выполнять тождественные преобразования алгебраических выражений.
Читать дальше: формула "квадрат суммы".









