Содержание:

Формулы

Первый способ. Чтобы найти площадь трапеции, нужно длину средней линии $l$ умножить на длину высоты $h$ опущенной к основанию (рис. 1):

$S=lh$

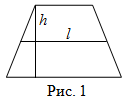
Напомним, что средней линией трапеции называется полусумма оснований.


Второй способ. Чтобы найти площадь трапеции, надо произведение ее диагоналей $d_1$ и $d_2$ умножить на синус угла $\beta$ между ними и поделить на два:

$$\mathrm{S}=\frac{1}{2} d_{1} d_{2} \sin \beta$$

Примеры вычисления площади трапеции

Пример

Задание. Найти площадь трапеции, основания которой равны 2 см и 4см, а высота 5 см.

Решение. Найдем длину средней линии трапеции:

$l=\frac{2+4}{2}=\frac{6}{2}=3$ (см)

Тогда искомая площадь равна:

$S=3 \cdot 5=15$ (см2)

Ответ. $S=15$ (см2)

Все формулы площади Калькулятор площади трапеции

Warning: file_put_contents(./students_count.txt): failed to open stream: Permission denied in /var/www/webmath-q2ws/data/www/webmath.ru/poleznoe/guide_content_banner.php on line 20
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 462 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Найти площадь трапеции, если длина ее одной диагонали равна 2 м, вторая диагональ в два раза больше, а угол между диагоналями равен $45^{\circ}$.

Решение. Найдем длину второй диагонали:

$d_2=2 \cdot 2=4$ (м)

Тогда искомая площадь

$S=\frac{1}{2} \cdot 2 \cdot 2 \cdot \sin 45^{\circ}=2 \cdot \frac{\sqrt{2}}{2}=\sqrt{2}$ (м2)

Ответ. $S=\sqrt{2}$ (м2)

Читать дальше: как найти площадь ромба.