Потенциальной энергией называют часть механической энергии совокупности тел (тела), которая зависит от взаимного расположения частей системы (конфигурации) и положения во внешнем поле сил.
Содержание:
- Определение и формула потенциальной энергии
- Выражения для потенциальной энергии
- Частные случаи формул для потенциальной энергии
- Единицы измерения потенциальной энергии
- Примеры решения задач
Определение и формула потенциальной энергии
Определение
Потенциальная энергия определяется работой, совершаемой потенциальными силами, которые действуют на все части системы, если система переходит из исследуемой конфигурации к состоянию, в котором считают потенциальную энергию равной нулю.А именно работа консервативных сил равна убыли потенциальной энергии. Начало отсчета потенциальной энергии делают произвольно. Эмпирически представляется возможным измерение только изменения потенциальной энергии. Начало отсчета потенциальной энергии делают так, чтобы упрощалось решение конкретной задачи.
Потенциальная энергия является скаляром. Чаще всего потенциальную энергию обозначают: Ep,Wp, U.
Потенциальную энергию системы (Ep) можно разделить на внешнюю: (Epvnesh) и внутреннюю потенциальные энергии Epvnesh . Тогда:
$$E_{p}=E_{p}^{\text {vnesh}}+E_{p}^{\text {vnutr}}(1)$$где Epvnesh получается как результат воздействия на систему со стороны тел, которые в рассматриваемую систему не входят. Epvnutr – вызвана взаимодействием разных частей составляющих систему.
Epvnutr является функцией координат всех материальных точек системы; Epvnesh помимо координат может в явном виде зависеть от времени.
Выражения для потенциальной энергии
Потенциальная энергия материальной точки находящейся в потенциальном поле сил определяют формулой:
$$d E_{p}=-d Y \rightarrow E_{p}=-Y+C$$где Y – силовая функция, C – постоянная интегрирования.
Консервативная сила ($\bar{F}$), которая действует на материальную точку связана с потенциальной энергией соотношением:
$$\bar{F}=-g \operatorname{rad} E_{p}=-\left(\frac{\partial E_{p}}{\partial x} \bar{i}+\frac{\partial E_{p}}{\partial y} \bar{j}+\frac{\partial E_{p}}{\partial z} \bar{k}\right)=-\bar{\nabla} E_{p}(3)$$где $\bar{\nabla}$ или $\nabla$ – оператор Гамильтона (оператор набла).
В случае нестационарных консервативных сил потенциальная энергия материальной точки является функцией координат и времени (Ep=Ep(x,y,z,t)).
Внутренняя потенциальная энергия системы – алгебраическая сумма потенциальных энергий (Ep(ik))взаимодействия всех пар точек системы:
$$\begin{aligned} E_{p}^{\text {vnutr}}=\sum_{i=1}^{n} \sum_{k>i}^{n} E_{p(i k)}=\frac{1}{2} \sum_{i=1}^{n} \sum_{k=1 \atop k \neq i}^{n} E_{p(i k)}(4) \\ & k \neq i \end{aligned}$$где $E_{p(i k)}=-\int \bar{F}_{i k} d \bar{r}_{i k}=-\int \bar{F}_{k i} d \bar{r}_{k i}=E_{p(k i)}, \bar{r}_{i k}=\bar{r}_{i}-\bar{r}_{k}, \bar{r}_{k i}=\bar{r}_{k}-\bar{r}_{i}$ , $\bar{F}_{i k}=-\bar{F}_{k i}$ –потенциальные силы с которыми взаимодействуют i–я и k-я точки системы. Если тело является твёрдым, то Epvnutr=const, тогда считают, что:
$$E_{p}=E_{p}^{\text {vnesh }}(5)$$Частные случаи формул для потенциальной энергии
Потенциальная энергия упруго деформированного в случае линейного растяжения тела наx равна:
$$E_{p}=\frac{k x^{2}}{2}(6)$$где k – коэффициент упругости.
Потенциальная энергия точки в поле гравитации Земли:
$$E_{p}=-\frac{G m M}{r}(r>R)(7)$$где m – масса материальной точки, M – масса Земли, R – радиус Земли. G – гравитационная постоянная. При этом полагают, что при $r \rightarrow \infty$ потенциальная энергия равна нулю $\left(E_{p}(\infty)=0\right)$.
Потенциальная энергия тела поднятого над Землей на расстояние много меньшее, чем радиус Земли равна:
$$E_{p}=m g h(8)$$где m – масса тела, g- ускорение свободного падения, h - высота поднятия тела ( от некоторого условно нулевого уровня, где потенциальная энергия считается равной нулю).
Единицы измерения потенциальной энергии
Основной единицей измерения кинетической энергии (как и любого другого вида энергии) в системе СИ служит Дж (джоуль), в системе СГС – эрг. При этом: 1 дж = 107 эрг.
Примеры решения задач
Пример
Задание. Материальная точка перемещается в положительном направлении оси X (x>0)в поле консервативных сил, потенциальная энергия которых задана графиком (рис.1). Как изменится в процессе движения модуль ускорения?
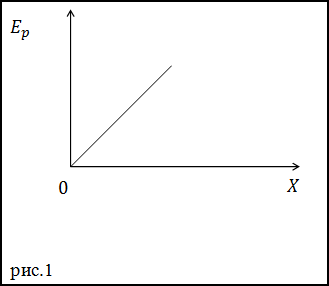
Решение. Исходя из графика на рис.1 можно записать уравнение, которое свяжет потенциальную энергию и координату материальной точки в ходе перемещения:
$$E_{p}=B x$$где A – некоторая постоянная.
В качестве основы для решения задачи используем формулу, связывающую консервативную силы и потенциальную энергию:
$$\bar{F}=-g r a d E_{p}(1.2)$$Для движения по оси X, которое представлено в нашей задаче выражение (1.2) примет вид:
$$\bar{F}=-\frac{d E_{p}}{d x} \bar{i}(1.3)$$Соответственно (1.1) и (1.3) модуль силы, действующей на материальную точку равен:
$$F=\frac{d}{d x}(B x)=B(1.4)$$По второму закону Ньютона модуль силы может быть найден как:
$$F = ma (1.5)$$Значит, получим выражение для ускорения рассматриваемой материальной точки:
$$a=\frac{B}{m}$$Ответ. Из полученного выражения для ускорения материально точки в заданном поле можно сделать вывод, что ускорение по модулю не изменяется.
Пример
Задание. Какую работу совершают над материальной точкой силы поля, если частица переходит из точки имеющей координаты (1;1;1) в точку с координатами (2;2;2). При этом потенциальная энергия частицы задана функцией: $E_{p}=x+y^{2}+2 z^{3}$ . Учтите, что потенциальная энергия задана в Дж, а координаты в метрах.
Решение. Потенциальная энергия определяется работой, совершаемой потенциальными силами, а именно работа консервативных сил равна убыли потенциальной энергии:
$$A=E_{p 1}-E_{p 2}(2.1)$$Используя условия задачи, найдем Ep1 и Ep2:
$$ \begin{array}{c} E_{p 1}=x+y^{2}+2 z^{3}=1+1+2=4 \\ E_{p 2}=x+y^{2}+2 z^{3}=2+2^{2}+2 \cdot 2^{3}=22 \end{array} $$Получаем:
$A = 4 - 22 = -18$ (Дж)
Ответ. A = -18 (Дж)
Читать дальше: Формула силы притяжения.










