Между любыми телами, которые обладают массами, действуют силы, которые притягивают вышеназванные тела друг к другу. Такие силы называют силами взаимного притяжения.

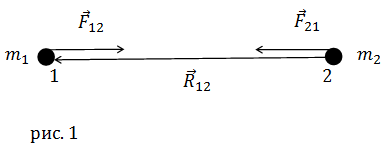
Рассмотрим две материальные точки (рис.1). Они притягиваются с силами прямо пропорциональными произведению масс этих материальных точек и обратно пропорциональными расстоянию между ними. Так, сила тяготения ( $\bar{F}_12$) будет равна:

$$ \bar{F}_{12}=-G \frac{m_{1} m_{2}}{r^{2}} \frac{\bar{r}_{12}}{r}(1) $$

где материальная точка массы m₂ действует на материальную точку массы m₁ с силой притяжения $\bar{F}_12$; $\bar{r}_12$ – радиус – вектор, который проведен из точки 2 в точку 1, модуль этого вектора равен расстоянию между материальными точками (r); G=6,67•10^-11 м³ кг^-1 с^-2(в системе СИ) – гравитационная постоянная (постоянная тяготения).

В соответствии с третьим законом Ньютона сила, с которой материальная точка 2 притягивается к материальной точке 1 ( $\bar{F}_21$) равна:

$$\bar{F}_{21}=-\bar{F}_{12}=G \frac{m_{1} m_{2}}{r^{2}} \frac{\bar{r}_{12}}{r}=-G \frac{m_{1} m_{2}}{r^{2}} \frac{\bar{r}_{21}}{r}(2)$$

где $\bar{r}_12 = - \bar{r}_21$

Тяготение между телами осуществляется посредством гравитационного поля (поля тяготения). Силы тяготения являются потенциальными. Это дает возможность ввести такую энергетическую характеристику гравитационного поля как потенциал, который равен отношению потенциальной энергии материальной точки, находящейся исследуемой точке поля к массе данной точки.

Формула для силы притяжения тел произвольной формы

В двух телах произвольной формы и размера выделим элементарные массы, которые можно считать материальными точками, причем:

$$d m_{1}=\rho_{1} d V_{1} \quad, d m_{2}=\rho_{2} d V_{2}$$

где $\rho_1, \rho_2$ – плотности вещества материальных точек первого и второго тел, dV₁ ,dV₂ - элементарные объемы выделенных материальных точек. В таком случае, сила притяжения ($d \bar{F}_12$), с которой элемент dm₂ действует на элемент dm₁, равна:

$$d \bar{F}_{12}=-G \frac{\rho_{1} \rho_{2} d V_{1} d V_{2}}{r_{12}^{3}} \bar{r}_{12}(4)$$

Следовательно, сила притяжения первого тела вторым может быть найдена по формуле:

$$\bar{F}_{12}=-G \int_{V_{1}} \rho_{1} d V_{1} \quad \int_{V_{2}} \frac{\rho_{2}}{r_{12}^{3}} \bar{r}_{12} d V_{2}$$

где интегрирование необходимо произвести по всему объему первого (V₁) и второго (V₂) тел. Если тела являются однородными, то выражение можно немного преобразовать и получить:

$$\bar{F}_{12}=-G \rho_{1} \rho_{2} \int_{V_{1}} d V_{1} \quad \int_{V_{2}} \frac{\bar{r}_{12}}{r_{12}^{3}} d V_{2}$$

Формула для силы притяжения твердых тел шарообразной формы

Если силы притяжения рассматриваются для двух твердых тел шарообразной формы (или близких к шарам), плотность которых зависит только от расстояний до их центров формула (6) примет вид:

$$\bar{F}_{12}=-G \frac{m_{1} m_{2}}{R^{3}} \bar{R}_{12}(7)$$

где m₁,m₂ – массы шаров, $\bar{R}_12$ – радиус – вектор, соединяющий центры шаров, $R=\left|\bar{R}_{12}\right|$

Выражение (7) можно использовать в случае, если одно из тел имеет форму отличную от шарообразной, но его размеры много меньше, чем размеры второго тела - шара. Так, формулой (7) можно пользоваться для вычислений сил притяжения тел к Земле.

Единицы измерения силы притяжения

Основной единицей измерения силы притяжения (как и любой другой силы) в системе СИ является: []=H.

В СГС: []=дин.

Примеры решения задач

Пример

Задание. Какова сила притяжения двух одинаковых однородных шара масса, которых равна по 1 кг? Расстояние между их центрами равно 1 м.

Решение. Основой для решения задачи служит формула:

$$\bar{F}_{g}=-G \frac{m_{1} m_{2}}{R^{3}} \bar{R}_{12}(1.1)$$

Для вычисления модуля силы притяжения формула (1.1) преобразуется к виду:

$$F_{g}=G \frac{m_{1} m_{2}}{R^{2}}$$

Проведем вычисления:

$F_{g}=6,67 \cdot 10^{-11} \frac{1 \cdot 1}{1^{2}}=6,67 \cdot 10^{-11}(H)$

Ответ. $F_{g}=6,67 \cdot 10^{-11}(H)$

Warning: file_put_contents(./students_count.txt): failed to open stream: Permission denied in /var/www/webmath-q2ws/data/www/webmath.ru/poleznoe/guide_content_banner.php on line 20

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 457 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. С какой силой (по модулю) бесконечно длинный и тонкий и прямой стержень притягивает материальную частицу массы m. Частица расположена на расстоянии a от стержня. Линейная плотность массы вещества стержня равна тау

Решение. Сделаем рисунок

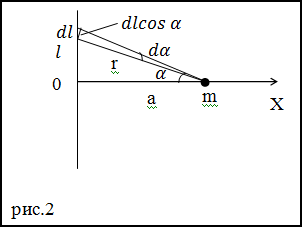
Выделим на стержне элементарный участок массы dm:

$$d m=\tau d l(2.1)$$

Силу притяжения между выделенным элементом на стержне и материальной точкой можно найти как:

$$d F=d F_{x}=G \frac{d m \cdot m}{r^{2}} \cos \alpha=G \frac{\tau d l \cdot m}{r^{2}} \cos \alpha$$

Из рис.2 очевидно, что:

$dlcos $\alpha=r d \alpha$ ( 2.3 )$

Подставим выражение (2.3) в (2.2), имеем:

$$d F=G \frac{\tau \cdot m}{r^{2}} r d \alpha=G \frac{\tau \cdot m}{r} d \alpha(2.4)$$

Из рис. 2 видно, что:

$$\frac{a}{r}=\cos \alpha \rightarrow r=\frac{a}{\cos \alpha}(2.5)$$

Подставим правую часть выражения (2.5) в формулу (2.4), получаем:

$$d F=G \frac{\tau \cdot m}{a} \cos \alpha d \alpha(2.6)$$

Для получения силы, с которой частица притягивается к стержню, проведем интегрирование выражения (2.6). Пределы интегрирования выберем от 0 до пи/2, так как стержень бесконечный умножим выражение на два для того, чтобы интегрирование было выполнено по всему объему стержня.

$$F=2 G \frac{\tau \cdot m}{a} \int_{0}^{\frac{\pi}{2}} \cos \alpha d \alpha=2 G \frac{\tau \cdot m}{a}$$

Ответ. $F=2 G \frac{\tau \cdot m}{a}$

Читать дальше: Формула силы трения.