Давление – это физическая величина,характеризующая состояние сплошной среды. Оно равно пределу отношения нормальной составляющей силы, которая действует на участок поверхности тела площади $\Delta S$ к размеру данной площади при $\Delta S \rightarrow 0$ . Обозначается давление буквой p. Тогда математической записью определения давления станет формула:
$$p=\lim _{\Delta S \rightarrow 0} \frac{\Delta F_{n}}{\Delta S}=\frac{d F_{n}}{d S}$$Содержание:
- Определение и формула давления
- Среднее давление
- Давление идеального газа
- Гидростатическое давление
- Единицы измерения давления
- Примеры решения задач
Определение и формула давления
Определение
Выражение (1) определяет давление в точке.
Среднее давление
Средним давлением на поверхность называют величину:
$$\langle p\rangle=\frac{F_{n}}{S}(2)$$где Fn – нормальная составляющая силы, которая действует на рассматриваемую поверхность, S – площадь этой поверхности.
Давление идеального газа
Давление идеального газа вычисляют, используя основное уравнение молекулярно – кинетической теории:
$$p=n k T(3)$$где $n=\frac{N}{V}$– концентрация молекул газа (N – число частиц), k=1,38•10-23 Дж/К – постоянная Больцмана, T – абсолютная температура газа.
Гидростатическое давление
Гидростатическое давление – давление внутри столба жидкости или газа, находится по формуле:
$$p=p_{0}+\rho g h(4)$$где $\rho$ – плотность вещества, g=9,8 м/с2 – ускорение свободного падения, h- высота столба вещества. p0 – внешнее давление на газ или жидкость.
Искривление поверхностного слоя жидкости ведет к возникновению дополнительного давления на жидкость, тогда давление под искривленной жидкостью определяется как:
$$p=p_{0}^{*}+2 \sigma H(5)$$где $\mathrm{P}_{0}^{*}$ –поверхностное натяжение жидкости,p0* – давление под не искривлённым слоем жидкости, H - средняя кривизна поверхности жидкости, вычисляемая по закону Лапласа:
$$H=\frac{1}{2}\left(\frac{1}{R_{1}}+\frac{1}{R_{2}}\right)$$R1, R2 – главные радиусы кривизны.
Единицы измерения давления
Основной единицей измерения давления в системе СИ является: [p]=Па (паскаль)
Внесистемные единицы давления: [p]=мм рт.ст.(миллиметр ртутного столба),мм в.ст (мм водяного столба),атмосфера,бар.
Па= Н/м2 и 1 бар=105 Па.
Техническая атмосфера ~1 бар. Физическая атмосфера 1,01 бар=760 мм рт.ст.. 1 мм рт.ст.=133 Па.
Примеры решения задач
Пример
Задание. Каково давление в море на глубине h=8,5 м, если атмосферное давление равно p0=105 Па, плотность морской воды равна $\rho$=1,03•103 кг/м3
Решение. Основой для решения задачи служит выражение:
$$p=p_{0}+\rho g h(1.1)$$Все данные в задаче указаны в системе СИ, поэтому можно провести вычисления:
$p=10^{5}+1,03 \cdot 10^{3} \cdot 9,8 \cdot 8,5=1,88 \cdot 10^{5}$ (Па).
Ответ. $p=1,88 \cdot 10^{5}$ (Па)
Пример
Задание. Каково давление струи на неподвижную плоскость, если струя воды ударяет ее под углом $\alpha$ к нормали плоскости, и упруго отскакивает от нее без изменения скорости? Скорость струи v.
Решение. Сделаем рисунок.
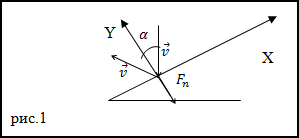
За время $\Delta t$ о стенку ударяется масса воды равная:
$$m=l S \rho=v \Delta t S \rho$$где S - поперечное сечение струи, $\rho$ – плотность воды. В соответствии с законом сохранения импульса имеем:
$$F \Delta t=m \Delta v \rightarrow F=\frac{m \Delta v}{\Delta t}(2.2)$$где F – сила, с которой вода действует на стенку.
Примем за положительное направление нормали внешней к опоре и учитывая, что струя отскакивает от стены без потери скорости, получаем:
$$\Delta v=v_{2} \cos \alpha-\left(-v_{1} \cos \alpha\right)=v_{2} \cos \alpha+v_{1} \cos \alpha=2 v \cos \alpha(2.3)$$Подставим $\Delta v$ из (2.3) в выражение (2.2), учтем выражение (2.1) имеем:
$$F=\frac{m 2 v \cos \alpha}{\Delta t}=\frac{v \Delta t S \rho 2 v \cos \alpha}{\Delta t}=2 \operatorname{Sov}^{2} \cos \alpha(2.4)$$В таком случае искомое давление струи на стенку будет равно:
$$p=\frac{F_{n}}{S}=2 \rho v^{2}$$Ответ. $p=2 \rho v^{2}$
Читать дальше: Формула закона Ома.










