Содержание:

Определение и формула закона Ома

Определение

Закон был получен Омом опытным путем. Построив вольт – амперную характеристику для проводника можно увидеть, что сила тока (I), текущего через проводник пропорциональна напряжению (U) на нем $(I \sim U)$.

Закон Ома для участка цепи

Если на рассматриваемом участке цепи, содержащей проводник, источников ЭДС нет $\left(U_{21}=\varphi_{1}-\varphi_{2}\right)$, то формула закона Ома является предельно простой:

$$I=\frac{U}{R}=\frac{\varphi_{1}-\varphi_{2}}{R}(1)$$

где R – сопротивление проводника (совокупности проводников, участка цепи).

Если источник тока в участок цепи включен и характеризуется при помощи ЭДС ($\varepsilon$), то формула закона Ома преобразуется к виду:

$$I=\frac{U}{R}=\frac{\varphi_{1}-\varphi_{2}+\varepsilon}{R}(2)$$

Закон Ома для замкнутой цепи

В том случае, если цепь является замкнутой, закон Ома принимает вид:

$$I=\frac{\varepsilon}{R}(3)$$

где под R=Rvnesh+rist понимают полное сопротивление цепи, которое включает так называемое внешнее сопротивление (Rvnesh) и сопротивление источника ЭДС (rist).

Формула закона Ома в дифференциальной форме

Все выше приведенные формулы закона Ома были представлены в интегральной форме. Этот закон можно записать в дифференциальной форме, которая характеризует электрическое состояние в точке.

$$\bar{j}=\sigma \bar{E}(4)$$

где $\sigma=\frac{1}{\rho}$ – удельная проводимость, $\rho$ – удельное сопротивление, $\bar{j}$ – вектор плотности тока, $\bar{E}$ – вектор напряженности электрического поля. Векторы $\bar{j}$ и $\bar{E}$ характеризуют одну точку проводящей среды. В том случае, если среда изотропна, то $\bar{j} \uparrow \uparrow \bar{E}$.

Примеры решения задач

Пример

Задание. Пространство между пластинами плоского конденсатора заполняет неоднородное плохо проводящее вещество, удельная проводимость которого изменяется в соответствии с линейным законом: $\sigma(r)=\sigma_{1}+\frac{\sigma_{2}-\sigma_{1}}{d} r$ в направлении перпендикулярном пластинам. d – расстояние между пластинами, S – площадь пластин конденсатора. Каким будет ток через этот конденсатор, если напряжение на нем станет равно U?

Решение. Сделаем рисунок.

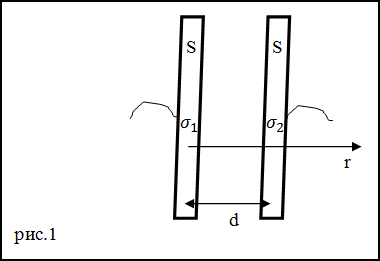
Для решения задачи используем формулу закона Ома в виде:

$$I=\frac{U}{R}(1.1)$$

Неизвестной величиной в выражении (1.1) является сопротивление конденсатора. Которое можно найти как сопротивление участка цепи между сечениями:

$$R=\int_{0}^{d} \rho \frac{d r}{S}=\int_{0}^{d} \frac{1}{\sigma} \frac{d r}{S}(1.2)$$

Для тог, чтобы найти полное сопротивление подставим заданное в условиях выражение для проводимости вещества в конденсаторе:

$$ \begin{array}{c} \left.R=\int_{0}^{d} \frac{1}{\left(\sigma_{1}+\frac{\sigma_{2}-\sigma_{1}}{d}\right.} r\right) \frac{d r}{S}=\frac{d}{S\left(\sigma_{2}-\sigma_{1}\right)}\left[\ln \left(d \sigma_{2}\right)-\ln \left(d \sigma_{1}\right)\right]= \\ =\frac{d}{S\left(\sigma_{2}-\sigma_{1}\right)} \ln \left(\frac{\sigma_{2}}{\sigma_{1}}\right)(1.2) \end{array} $$

Подставим найденное в (1.2) сопротивление в (1.1), получим искомую силу тока:

$I=\frac{U}{\frac{d}{S\left(\sigma_{2}-\sigma_{1}\right)} \ln \left(\frac{\sigma_{2}}{\sigma_{1}}\right)}=\frac{U S\left(\sigma_{2}-\sigma_{1}\right)}{d \cdot \ln \left(\frac{\sigma_{2}}{\sigma_{1}}\right)}$

Ответ. $I=\frac{U S\left(\sigma_{2}-\sigma_{1}\right)}{d \cdot \ln \left(\frac{\sigma_{2}}{\sigma_{1}}\right)}$


Warning: file_put_contents(./students_count.txt): failed to open stream: Permission denied in /var/www/webmath-q2ws/data/www/webmath.ru/poleznoe/guide_content_banner.php on line 20
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 471 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Какой будет плотность тока в металлическом проводнике (удельное сопротивление считать равным $\rho$) постоянного сечения, имеющем длину l, если напряжение, которое приложено к проводу равно U?

Решение. Плотность тока для проводника, который имеет постоянное сечение S можно найти как:

$$j=\frac{I}{S}(2.1)$$

Силу тока можно вычислить, если использовать формулу Закона Ома для участка цепи не имеющего ЭДС:

$$I=\frac{U}{R}(2.2)$$

Сопротивление провода найдем, применяя формулу:

$$R=\rho \frac{l}{S}(2.3)$$

Подставим, необходимые величины в (2.1), получим:

$$j=\frac{U}{S R}=\frac{U S}{S \rho l}$$

Ответ. $j=\frac{U S}{S \rho l}$


Читать дальше: Формула мощности тока.