Ускорением (мгновенным ускорением) называют вектор, который определяет быстроту, с которой изменяется скорость перемещающейся материальной точки.
Содержание:
- Определение и формула ускорения
- Единицы измерения ускорения
- Виды ускорения
- Формула ускорения в разных системах координат
- Примеры решения задач
Определение и формула ускорения
Определение
Обычно ускорение обозначают $\bar{a}$. В теоретической механике встречается обозначение ускорения: $\bar{w}$. Математическим определением мгновенного ускорения являются выражения:
$$\bar{a}=\frac{d \bar{v}}{d t}=\dot{\bar{v}}(1)$$где $\bar{v}$ – скорость движения материальной точки
или
$$\bar{a}=\frac{d^{2} \bar{r}}{d t^{2}}=\ddot{\bar{r}}(2)$$где $\bar{r}$ – радиус – вектор, который определяет положение материальной точки в пространстве.
Вектор ускорения располагается в плоскости соприкосновения, в которой находится главная нормаль и касательная к траектории, при этом он имеет направление в сторону вогнутости траектории.
Единицы измерения ускорения
Основными единицами измерения ускорения в системе СИ является: [a]=м/с2
в СГС: [a]=см/с2
Виды ускорения
Если построить соприкасающуюся плоскость, в любой точке траектории, то вектор $\bar{a}$ разложим на две взаимно перпендикулярные составляющие:
$$\bar{a}=\bar{a}_{n}+\bar{a}_{\tau}(3)$$где $\bar{a}_n$ - вектор, направленный по главной нормали к центру кривизны траектории материальной точки – это нормальное ускорение; $\bar{a}_{\tau}$ - вектор, направленный по касательной к траектории – это касательное ускорение. При этом выполняются равенства:
$$a_{n}=\frac{v^{2}}{R}(4)$$ $$a_{\tau}=\frac{d}{d t}|\bar{v}|(5)$$ $$|\bar{a}|=a=\sqrt{a_{\tau}^{2}+a_{n}^{2}}=\sqrt{\left(\frac{v^{2}}{R}\right)^{2}+\dot{v}^{2}}(6)$$где $|\bar{v}|=v$ – модуль вектора скорости, R – радиус кривизны траектории, an – проекция вектора $\bar{a}_n$ на направление единичного вектора главной нормали $(\bar{n})$, aт – проекция вектора $\bar{a}_{\tau}$ на направление единичного вектора касательной $\left(\bar{\tau}=\frac{\bar{v}}{v}\right)$. Величина an определяет быстроту изменения направления скорости, а величина aт - быстроту изменения модуля скорости.
Если $a_{\tau}=0$, то такое движение называют равномерным. При $a_{\tau}=$ const движение является равнопеременным (при $a_{\tau} < 0$ равнозамедленным, при $a_{\tau} > 0$ равноускоренным).
Средним ускорением материальной точки $\langle\bar{a}\rangle$ на отрезке времени от $t$ до $t+\Delta t$ называется векторная величина, равная отношению:
$$\langle\bar{a}\rangle(t, \Delta t)=\frac{\Delta \bar{v}}{\Delta t}=\frac{\bar{v}(t+\Delta t)-\bar{v}(t)}{\Delta t}(7)$$При $\Delta t \rightarrow 0$ в пределе среднее ускорение совпадает с мгновенным ускорением:
$$\lim _{\Delta t \rightarrow 0}\langle\bar{a}\rangle(t, \Delta t)=\lim _{\Delta t \rightarrow 0} \frac{\Delta \bar{v}}{\Delta t}=\frac{d \bar{v}}{d t}=\bar{a}(t)(8)$$Формула ускорения в разных системах координат
В декартовых координатах проекции ускорения (ax,ay,az) на оси (X,Y,Z)можно представить как:
$$a_{x}=\dot{v}_{x}=\ddot{x}, \quad a_{y}=\dot{v}_{y}=\ddot{y}, a_{z}=\dot{v}_{z}=\ddot{z}(9)$$Соответственно, имеем:
$$\bar{a}=\ddot{x i}+\ddot{y} \bar{j}+\ddot{z} \bar{k}(10)$$где $\bar{i}, \bar{j}, \bar{k}$ – единичные орты по осям X,Y.Z. При этом модуль ускорения равен:
$$|\bar{a}|=a=\sqrt{a_{x}^{2}+a_{y}^{2}+a_{z}^{2}}=\sqrt{\ddot{x}^{2}+\ddot{y}^{2}+\ddot{z}^{2}}(11)$$В цилиндрической системе координат имеем:
$$a=\sqrt{\left(\ddot{\rho}-\rho \dot{\varphi}^{2}\right)^{2}+(\rho \ddot{\varphi}+2 \dot{\rho} \dot{\varphi})^{2}+\ddot{z}^{2}}(12)$$В сферической системе координат модуль ускорения можно найти как:
$$ \begin{array}{c} a=\left[\left(\ddot{r}-r \dot{\varphi}^{2} \sin ^{2} \theta-r \dot{\theta}^{2}\right)^{2}+(2 \dot{r} \dot{\varphi} \sin \theta+r \ddot{\varphi} \sin \theta+2 r \dot{\theta} \dot{\varphi} \cos \theta)^{2}\right. \\ +\left(2 \dot{r} \dot{\theta} \sin \theta+r \ddot{\theta}-2 r \dot{\varphi}^{2} \sin \theta \cos \theta\right)^{2} \frac{1}{2}(13) \end{array} $$Примеры решения задач
Пример
Задание. Материальная точка движется по окружности (рис.1), которая имеет радиус R=2м, уравнение движения: $S=10 t-2,5 t^{2}$, где t в секундах, а S в метрах. Каков модуль ускорения данной точки при t=3 c?
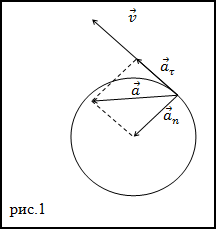
Решение. В качестве основы для решения задачи используем формулу:
$$|\bar{a}|=a=\sqrt{a_{\tau}^{2}+a_{n}^{2}}=\sqrt{\left(\frac{v^{2}}{R}\right)^{2}+\dot{v}^{2}}(1.1)$$Используя заданное уравнение движения, найдем модуль скорости материальной точки:
$$v(t)=\frac{d S}{d t}=10-5 t$$Продифференцировав уравнение для модуля скорости (1.2) по времени получим тангенциальную составляющую ускорения:
$a_{\tau}=-5$ м/с2
Для вычисления нормальной составляющей скорости движения нашей материальной точки следует, используя выражение (1.2) найти:
$a_{n}=\frac{v^{2}(t=3)}{R}=\frac{(10-5 \cdot 3)^{2}}{2}=12,5$ м/с2
Используя выражение (1.1) вычислим искомое ускорение:
$a=\sqrt{(-5)^{2}+(12,5)^{2}} \approx 13,5$ м/с2
Ответ. $a=\approx 13,5$ м/с2
Пример
Задание. Какова зависимость ускорения материальной точки от времени (a(t)), если частица перемещается по оси X и ее скорость изменяется в соответствии с уравнением: $v=\alpha \sqrt{x}$, где $\alpha$ – постоянная большая нуля? В начальный момент времени (при t=0 с) материальная точка находилась в начале координат (x=0 м). Нарисуйте график a(t).
Решение. Из условий задачи можно записать, что:
$$v=v_{x}=\alpha \sqrt{x}=\frac{d x}{d t}(2.1)$$Используя формулу (2.1) найдем зависимость координаты xот времени (x(t) ):
$$\int \alpha d t=\int \frac{d x}{\sqrt{x}} \rightarrow \alpha t=2 \sqrt{x}+C(2.2)$$где постоянную интегрирования найдем из начального условия задачи. Мы знаем, что x(0)=0, значит C=0. Имеем:
$$x(t)=\frac{1}{4} \alpha^{2} t^{2}(2.3)$$Используя формулу для нахождения ускорения для нашего случая (движение по оси X):
$$a=a_{x}=\ddot{x}(2.4)$$получим искомое выражение для a(t):
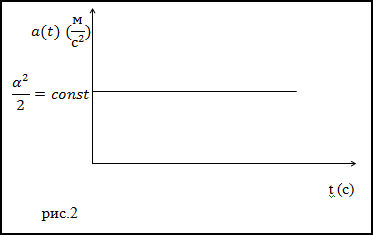
$$a(t)=\frac{\alpha^{2}}{2}$$Ответ. $a(t)=\frac{\alpha^{2}}{2}$ ускорение от времени не зависит, значит, график a(t) принимает вид (рис.2).
Читать дальше: Формула давления.










