Плотностью вещества (плотностью вещества тела) называют скалярную физическую величину, которая равна отношению массы (dm) малого элемента тела к его единичному объему (dV). Чаще всего плотность вещества обозначают греческой буквой $\rho$. И так:
$$\rho=\frac{d m}{d V}$$Содержание:
- Определение и формула плотности вещества
- Виды плотности вещества
- Единицы измерения плотности вещества
- Примеры решения задач
Определение и формула плотности вещества
Определение
Виды плотности вещества
Применяя выражение (1) для определения плотности, говорят о плотности тела в точке.
Плотность тела зависит от материала тела и его термодинамического состояния.
В том случае, если тело можно считать однородным (плотность вещества во всем теле одинакова ( $\rho = const$), то $\rho$ определяют следующей формулой:
$$\rho=\frac{m}{V}$$где m – масса тела, V – объем тела.
Если тело является неоднородным, то иногда пользуются понятием средней плотности $\langle\rho\rangle$, которая рассчитывается как:
$$\langle\rho\rangle=\frac{m}{V}(3)$$где m – масса тела, V – объем тела. В технике для неоднородных (например, сыпучих) тел используют понятие объемной плотности. Объемную плотность рассчитывают так же как $\langle\rho\rangle=\frac{m}{V}(3)$ (3). Объем определяют, включая промежутки в сыпучих и рыхлых материалах (таких как: песок, гравий, зерно и т.д.).
При рассмотрении газов, находящихся в нормальных условиях для вычисления плотности применяют формулу:
$$\rho=\frac{\mu}{V_{\mu}}(4)$$где $\mu$ – молярная масса газа, $V_{\mu}$ – молярный объем газа, который при нормальных условиях составляет 22,4 л/моль.
Единицы измерения плотности вещества
В соответствии с определением, можно записать, что единицами измерения плотности в системе СИ служит: [$\rho$]=кг/м3
в СГС: [$\rho$]=г/(см)3
При этом: 1 кг/м3 = (10)-3 г/(см)3 .
Примеры решения задач
Пример
Задание. Какова плотность воды, если объем, который занимает одна молекула H2O, примерно равен $\Delta V \approx 3 \cdot 10^{-29}$ м3? Считайте, что молекулы в воде плотно упакованы.
Решение. Если считать, что молекулы в воде плотно упакованы, то ее плотность можно найти как:
$$\rho=\frac{m_{0}}{\Delta V}$$где m0 – масса молекулы воды. Найдем m0, используя известное соотношение:
$$\frac{m}{\mu}=\frac{N}{N_{A}}$$где N=1 - количество молекул (в нашем случае одна молекула), m - масса рассматриваемого количества молекул (в нашем случае m=m0), NА=6,02• 1023 моль-1 – постоянная Авогадро, $\mu$=18•10-3 кг/моль (так как относительная молекулярная масса воды равна Mr=18). Следовательно, применяя выражение (2) для нахождения массы одной молекулы имеем:
$$m_{0}=\frac{\mu}{N_{A}}(3)$$Подставим m0 в выражение (1), получаем:
$$\rho=\frac{\mu}{\Delta V N_{A}}(4)$$Проведем расчет искомой величины:
$\rho=\frac{18 \cdot 10^{-3}}{3 \cdot 10^{-29} \cdot 6,02 \cdot 10^{23}}=10^{3} \mathrm{kr} / \mathrm{m}^{3}$ кг/м3
Ответ. Плотность воды равна 103 кг/м3 .
Пример
Задание. Какова плотность кристаллов хлорида цезия (CsCl), если кристаллы имеют кубическую кристаллическую решетку (рис.1) в вершинах которой находятся ионы хлора (Cl-), а в центре расположен ион цезия (Cs+). Ребро кристаллической решетки считайте равным d=0, 41 нм.
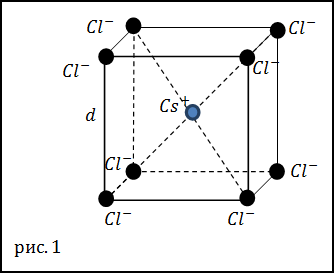
Решение. За основу решения задачи примем выражение:
$$\frac{m}{\mu}=\frac{N}{N_{A}}(2.1)$$где m – масса вещества (в нашем случае это масса одной молекулы $\left.\operatorname{CsCl}\left(m_{0}\right)\right), N=1, N_{A}=6,02 \cdot 10^{23}$ – постоянная Авогадро, $\mu=168 \cdot 10^{-3}$ кг/моль молярная масса хлорида Цезия (так как относительная молекулярная хлорида цезия равна $M_r = 168$). Выражение (2.1) для одной молекулы примет вид:
$$\frac{m_{0}}{\mu}=\frac{1}{N_{A}}$$В выражении (2.2) массу молекулы можно выразить через ее плотность как:
$$m_{0}=\rho V_{m}(2.3)$$где Vm – объем исследуемой молекулы. Так как кристаллы имеют кубическую кристаллическую решетку, ребро которой нам известно (и равно d), то вместо объема Vm можно использовать выражение:
$$V_{m}=d^{3}(2.4)$$Подставим выражения (2.3) и (2.4) в формулу (2.2), получим:
$$\frac{\rho V_{m}}{\mu}=\frac{1}{N_{A}}(2.5)$$Тогда выражение для плотности примет вид:
$$\rho=\frac{\mu}{d^{3} N_{A}}$$Переведем размер стороны кристаллической решетки в единицы системы СИ, получим d=0,41нм=0, 41•10-9) м. Проведем вычисления:
$\rho=\frac{168 \cdot 10^{-3}}{\left(0,41 \cdot 10^{-9}\right)^{3} \cdot 6,02 \cdot 10^{23}}=4047,6$ кг/м3
Ответ. $\rho=4047,6$ кг/м3
Читать дальше: Формула потенциальной энергии.










