Исходя из формулы (1) силу тяги можно определить через полезную мощность, и скорость транспортного средства (v):
$$F_{T}=\frac{P}{v}(2)$$Содержание:
В том случае, если тело при перемещении имеет ускорение, то на него кроме всех прочих обязательно действует некоторая сила, которая является силой тяги в рассматриваемый момент времени. В действительности, если тело движется прямолинейно и с постоянной скоростью, то сила тяги также действует, так как тело должно преодолевать силы сопротивления. Обычно силу тяги находят, рассматривая силы, действующие на тело, находя равнодействующую и применяя второй закон Ньютона. Жестко определенной формулы для силы тяги не существует.
Не следует считать, что сила тяги, например, транспортного средства действует со стороны двигателя, так как внутренние силы не могут менять скорость системы как единого целого, что входило бы в противоречие с законом сохранения импульса. Однако следует отметить, что для получения у силы трения покоя необходимого направления, мотор вращает колеса, колеса «цепляются за дорогу» и порождается сила тяги. Теоретически было бы возможно не использовать понятие «сила тяги», а говорить о силе трения покоя или силе реакции воздуха. Но удобнее внешние силы, которые действуют на транспорт делить на две части, при этом одни силы называть силами тяги $(/bar{F}_T)$, а другие - силами сопротивления $\bar{F}_S$ . Это делается для того, чтобы уравнения движения не потеряли свой универсальный вид и полезная механическая мощность (P) имела простое выражение:
$$P=\bar{F}_{T} \bar{v}(1)$$Определение и формула силы тяги
Определение
Для автомобиля, поднимающегося в горку, которая имеет уклон
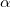, масса автомобиля m сила тяги (FT) войдет в уравнение:
где a – ускорение, с которым движется автомобиль.
Единицы измерения силы тяги
Основной единицей измерения силы в системе СИ является: [FT]=Н
В СГС: [FT]=дин
Примеры решения задач
Пример
Задание. На автомобиль имеющий массу 1 т при его движении по горизонтальной поверхности, действует сила трения, которая равна $\mu$=0,1 от силы тяжести. Какой будет сила тяги, если автомобиль движется с ускорением 2 м/с?
Решение. Сделаем рисунок.
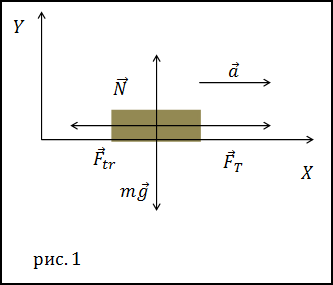
В качестве основы для решения задачи используем второй закон Ньютона:
$$\bar{N}+m \bar{g}+\bar{F}_{t r}+\bar{F}_{T}=m \bar{a}(1.1)$$Спроектируем уравнение (1.1) на оси X и Y:
$$ \begin{array}{c} X: F_{T}-F_{t r}=m a(1.2) \\ Y: m g=N(1.3) \end{array} $$По условию задачи:
$$ F_{t r}=\mu \cdot m g (1.4) $$Подставим правую часть выражения (1.4) вместо силы трения в (1.2), получим:
$$F_{T}=m a+\mu \cdot m g$$Переведем массу в систему СИ m=1т=103 кг, проведем вычисления:
$$F_{T}=10^{3}(2+0,1 \cdot 9,8)=2,98 \cdot 10^{3}(H)$$Ответ. FT=2,98 кН
Warning: file_put_contents(./students_count.txt): failed to open stream: Permission denied in /var/www/webmath-q2ws/data/www/webmath.ru/poleznoe/guide_content_banner.php on line 20
Пример
Задание. На гладкой горизонтальной поверхности лежит доска массой M. На доске находится тело массы m. Коэффициент трения тела о доску равен $\mu$ . К доске приложена сила горизонтальная сила тяги, которая зависит от времени как: F=At (где A=const). В какой момент времени доска начнет выскальзывать из-под тела?
Решение. Сделаем рисунок.
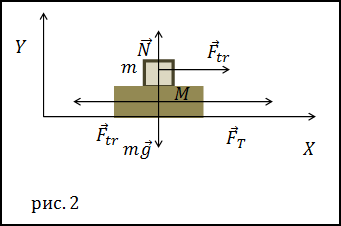
Для решения задачи нам потребуются проекции сил на осиX и Y, которые отличны от нуля. Для тела массы m:
$$ \begin{array}{c} X: m a_{1}=F_{t r}(2.1) \\ Y: m g=N(2.2) \\ F_{t r}=\mu N=\mu m g \rightarrow m a_{1}=\mu m g \rightarrow a_{1}=\mu g(2.3) \end{array} $$Для тела массы M:
$$M a_{2}=F-F_{t r} \rightarrow M a_{2}=A t-F_{t r} \rightarrow a_{2}=\frac{A t-F_{t r}}{M}(2.2)$$Обозначим момент времени, в который доска начнет выскальзывать из-под тела t0, тогда
$$\mu g=\frac{A t_{0}-\mu m g}{M} \rightarrow t_{0}=\frac{m+M}{A} \mu g$$Ответ. $t_{0}=\frac{m+M}{A} \mu g$
Читать дальше: Формула силы упругости.
Статьи по теме
Поможем выполнить
любую работу
