Содержание:

При действии на тело внешней силы онодеформируется (происходит изменение размеров, объема и часто формы тела). В ходе деформации твердого тела возникают смещения частиц, находящихся в узлах кристаллической решетки из начальных положений равновесия в новые положения. Такому сдвигу препятствуют силы, с которыми частицы взаимодействуют. В результате появляются внутренние силы упругости, уравновешивающие внешние силы. Эти силы приложены к деформированному телу. Величина сил упругости пропорциональна деформации тела.

Определение и формула силы упругости

Определение

Силой упругости называют силу, имеющую электромагнитную природу, которая возникает в результате деформации тела, как ответ на внешнее воздействие.

Упругой называют деформацию, при которой после прекращения действия внешней силы тело восстанавливает свои прежние форму и размеры, деформация исчезает. Деформация носит упругий характер только в том случае, если внешняя сила не превышает некоторого определенного значения, называемого пределом упругости. Сила упругости при упругих деформациях является потенциальной. Направление вектора силы упругости противоположно направлению вектора перемещения при деформации. Или по-другому можно сказать, что сила упругости направлена против перемещения частиц при деформации.

Характеристики упругих свойств твердых тел

Упругие свойства твердых тел характеризуют при помощи напряжения, которое часто обозначают буквой $\sigma$ . Напряжение – это физическая величина, равная упругой силе, которая приходится на единичное сечение тела:

$$\sigma=\frac{d F_{u p r}}{d S}(1)$$

где dFupr – элемент силы упругости тела; dS – элемент площади сечения тела. Напряжение называется нормальным, если вектор $d \bar{F}_{u p r}$ перпендикулярен к dS.

Формулой для расчета силы упругости служит выражение:

$$d F_{u p r}=\sigma d S=K \frac{\Delta x}{x} d S(2)$$

где $\frac{\Delta x}{x}$ - относительная деформация, $\Delta x$ – абсолютная деформация, x–первоначальное значение величины, которая характеризовала форму или размеры тела; K – модуль упругости ( $k = \sigma$ при ( $\frac{\Delta x}{x} = 1$ ). Величину обратную модулю упругости называют коэффициентом упругости. Проще говоря, сила упругости по величине пропорциональная величине деформации.

Продольное растяжение (сжатие)

Продольное (одностороннее) растяжение состоит в том, что под действием растягивающей (сжимающей) силы происходит увеличение (уменьшение) длины тела. Условием прекращения такого рода деформации является выполнение равенства:

$F = F_{upr} (3)$

где F – внешняя сила, приложенная к телу, Fupr – сила упругости тела. Мерой деформации в рассматриваемом процессе является относительное удлинение (сжатие) $\left(\frac{\Delta l}{l}\right)$ .

Тогда модуль силы упругости можно определить как:

$$F_{u p r}=E \frac{\Delta l}{l} S(4)$$

где E – модуль Юнга, который в рассматриваемом случае равен модулю упругости (E=K) и характеризующий упругие свойства тела; l – первоначальная длина тела; $\Delta l$ – изменение длины при нагрузке F=F_upr. При $\Delta l=l E=\frac{F}{S}=\sigma$ – площадь поперечного сечения образца.

Выражение (4) называют законом Гука.

В простейшем случае рассматривают силу упругости, которая возникает при растяжении (сжатии) пружины. Тогда закон Гука записывают как:

$$F_{x}=k x(5)$$

где Fx – модуль проекции силы упругости; k – коэффициент жесткости пружины, x – удлинение пружины.

Деформация сдвига

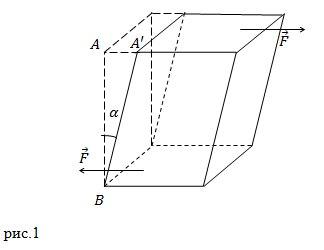
Сдвигом называют деформацию, при которой все слои тела, являющиеся параллельными некоторой плоскости, смещаются друг относительно друга. При сдвиге объем тела, которое было деформировано, не изменяется. Отрезок, на который смещается одна плоскость относительно другой, называют абсолютным сдвигом (рис.1 отрезок AA’). Если угол сдвига ($\alpha$) мал, то $\alpha \approx t g \alpha=\frac{A A^{\prime}}{A B}$ . Этим углом ? (относительный сдвиг) характеризуют относительную деформацию. При этом напряжение $\sigma$ равно:

$$\sigma=G \alpha(6)$$

где G – модуль сдвига.

Единицы измерения силы упругости

Основной единицей измерения сил упругости (как и любой другой силы) в системе СИ является: [Fupr]=H

В СГС: [Fupr]=дин

Примеры решения задач

Пример

Задание. Какова работа силы упругости при деформации пружины жёсткость, которой равна k? Если первоначальное удлинение пружины составляло x1, последующее удлинение составило x2.

Решение. В соответствии с законом Гука модуль силы упругости найдем как:

$$F = kx (1.1)$$

При этом сила упругости при первой деформации будет равна:

$$F_1 = kx_1 (1.2)$$

В случае второй деформации имеем:

$$F_2 = kx_2 (1.3)$$

Работу (A) сил упругости можно найти как:

$$A=\langle F\rangle S \cos \alpha(1.4)$$

где $\langle F\rangle$ - средняя величина силы упругости, равная:

$$\langle F\rangle=\frac{F_{1}+F_{2}}{2}(1.5)$$

S- модуль перемещения, равный:

$S = x_2 - x_1 (1.6)$

$\alpha=180^{\circ}$ - угол между векторами перемещения и вектором сил упругости (эти векторы направлены в противоположные стороны). Подставим выражения (1.2), (1.3), (1.5) и (1.6) в формулу для работы (1.4), получим:

$$A=\frac{k x_{1}+k x_{2}}{2}\left(x_{2}-x_{1}\right) \cos \left(180^{\circ}\right)=-\frac{k x_{1}+k x_{2}}{2}\left(x_{2}-x_{1}\right)$$

Ответ. $A=-\frac{k}{2}\left(x_{1}+x_{2}\right)\left(x_{2}-x_{1}\right)$


Warning: file_put_contents(./students_count.txt): failed to open stream: Permission denied in /var/www/webmath-q2ws/data/www/webmath.ru/poleznoe/guide_content_banner.php on line 20
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 447 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Тело массой m (которое можно считать материальной точкой) привязано к резиновому шнуру. Это тело описывает в горизонтальной плоскости окружность с частотой вращения n. Угол отклонения шнура от вертикали равен $\alpha$. Жёсткость шнура равна k. Какова длина нерастянутого шнура (l0)?

Решение. Сделаем рисунок.

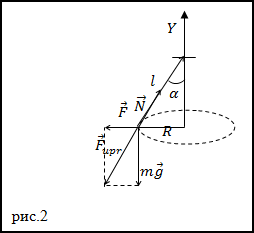
Сила натяжения (N) шнура вызывает его растяжениена величину ($\Delta l$). При этом возникающая сила упругости равна по модулю и противоположна по направлению силе натяжения:

$$\bar{F}_{u p r}=-\bar{N}(2.1)$$

Сила натяжения шнура равна (из рис.2 и второго закона Ньютона):

$$N=\frac{m g}{\cos \alpha}(2.2)$$

Но так как сила натяжения равна по модулю силе упругости, то можно записать, что:

$$N=k \Delta l \rightarrow \Delta l=\frac{N}{k}(2.3)$$

Рассмотрение рис.2 дает:

$$\frac{l}{R}=\frac{N}{F} \rightarrow l=\frac{N R}{F}(2.4)$$

где l – длина растянутой нити, R – радиус окружности по которой движется точка. Применяя второй закон Ньютона, получим:

$$F=N \sin \alpha=m \frac{v^{2}}{R}=4 \pi^{2} n^{2} m R(2.5)$$

Подставим в (2.4) выражение для F, получаем:

$$l=\frac{N}{4 \pi^{2} n^{2} m}(2.6)$$

В таком случае длина нерастянутого шнура:

$$l_{0}=l-\Delta l=\frac{N}{4 \pi^{2} n^{2} m}-\frac{N}{k}=\left(\frac{1}{4 \pi^{2} n^{2} m}-\frac{1}{k}\right) \frac{m g}{\cos \alpha}$$

Ответ. $l_{0}=\left(\frac{1}{4 \pi^{2} n^{2} m}-\frac{1}{k}\right) \frac{m g}{\cos \alpha}$


Читать дальше: Формула скорости.