Сила $\bar{F}$ , действующая на движущуюся заряженную частицу в магнитном поле, равная:
$$\bar{F}=q[\bar{v} \times \bar{B}](1)$$называется силой Лоренца (магнитной силой).
Содержание:
Определение
Сила $\bar{F}$ , действующая на движущуюся заряженную частицу в магнитном поле, равная:
$$\bar{F}=q[\bar{v} \times \bar{B}](1)$$называется силой Лоренца (магнитной силой).
Исходя из определения (1) модуль рассматриваемой силы:
$$F=q v B \sin \alpha(2)$$где $\bar{v}$ – вектор скорости частицы, q – заряд частицы, $\bar{B}$ – вектор магнитной индукции поля в точке нахождения заряда, $\alpha$ – угол между векторами $\bar{v}$ и $\bar{B}$. Из выражения (2) следует, что если заряд движется параллельно силовым линиям магнитного поля,то сила Лоренца равна нулю. Иногда силу Лоренца стараясь выделить, обозначают, используя индекс: $\bar{F}_L$
Сила Лоренца (как и всякая сила) – это вектор. Ее направление перпендикулярно вектору скорости
$\bar{v}$ и вектору
$\bar{B}$ (то есть перпендикулярно плоскости, в которой находятся векторы скорости и магнитной
индукции) и определяется правилом правого буравчика (правого винта) рис.1 (a). Если мы имеем дело с отрицательным зарядом,
тонаправление силы Лоренца противоположно результату векторного произведения
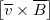 (рис.1(b)).
(рис.1(b)).
вектор $\bar{B}$ направлен перпендикулярно плоскости рисунков на нас.
Так как сила Лоренца направлена всегда перпендикулярно направлению скорости заряда, то ее работа над частицей равна нулю. Получается, что воздействуя на заряженную частицу при помощи постоянного магнитного поля нельзя изменить ее энергию.
Если магнитное поле однородно и направлено перпендикулярно скорости движения заряженной частицы, то заряд под воздействием силы Лоренца будет перемещаться по окружности радиуса R=const в плоскости, которая перпендикулярна вектору магнитной индукции. При этом радиус окружности равен:
$$R=\frac{m \gamma v}{|q| B}(3)$$где m – масса частицы,|q|- модуль заряда частицы, $\gamma=\frac{1}{\sqrt{1-\frac{v^{2}}{c^{2}}}}$ – релятивистский множитель Лоренца, c – скорость света в вакууме.
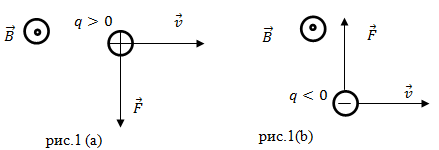
Сила Лоренца - это центростремительная сила. По направлению отклонения элементарной заряженной частицы в магнитном поле делают вывод о ее знаке (рис.2).
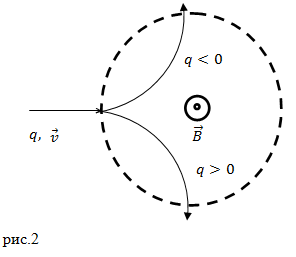
Если заряженная частица перемещается в пространстве, в котором находятся одновременно два поля (магнитное и электрическое), то сила, которая действует на нее, равна:
$$\bar{F}=q \bar{E}+q[\bar{v} \times \bar{B}](4)$$где $\bar{E}$ – вектор напряженности электрического поля в точке, в которой находится заряд. Выражение (4) было эмпирически получено Лоренцем. Сила $\bar{F}$, которая входит в формулу (4) так же называется силой Лоренца (лоренцевой силой). Деление лоренцевой силы на составляющие: электрическую $(\bar{F} = q \bar{E})$ и магнитную $(\bar{F}=q[\bar{v} \times \bar{B}])$ относительно, так как связано с выбором инерциальной системы отсчета. Так, если система отсчета будет двигаться с такой же скоростью $\bar{v}$, как и заряд, то в такой системе сила Лоренца, действующая на частицу, будет равна нулю.
Основной единицей измерения силы Лоренца (как и любой другой силы) в системе СИ является: [F]=H
В СГС: [F]=дин
Пример
Задание. Какова угловая скорость электрона, который движется по окружности в магнитном поле с индукцией B?
Решение. Так как электрон (частица имеющая заряд) совершает перемещение в магнитном поле, то на него действует сила Лоренца вида:
$$\bar{F}=q[\bar{v} \times \bar{B}](1.1)$$где q=qe – заряд электрона. Так как в условии сказано, что электрон движется по окружности, то это означает, что $\bar{v} \perp \bar{B}$, следовательно, выражение для модуля силы Лоренца примет вид:
$$F=q v B(1.2)$$Сила Лоренцаявляется центростремительной и кроме того, по второму закону Ньютона будет в нашем случае равна:
$$F=m a_{n}=m \frac{v^{2}}{R}(1.3)$$Приравняем правые части выражений (1.2) и (1.3), имеем:
$$q v B=m \frac{v^{2}}{R}(1.4)$$Из выражения (1.3) получим скорость:
$$v=\frac{q B R}{m}(1.5)$$Период обращения электрона по окружности можно найти как:
$$T=\frac{2 \pi R}{v}=\frac{2 \pi m}{q B}(1.6)$$Зная период, можно найти угловую скорость как:
$$\omega=\frac{2 \pi}{T}=\frac{q_{e} B}{m}$$Ответ. $\omega=\frac{q_{e} B}{m}$
Пример
Задание. Заряженная частица (заряд q, масса m) со скоростью vвлетает в область, где имеется электрическое поле напряженностью E и магнитное поле с индукцией B. Векторы $\bar{E}$ и $\bar{B}$ совпадают по направлению. Каково ускорение частицы в моментначалаперемещения в полях, если $\bar{v} \uparrow \bar{B} \uparrow \bar{E}$?
Решение. Сделаем рисунок.
На заряженную частицу действует сила Лоренца:
$$\bar{F}=q \bar{E}+q[\bar{v} \times \bar{B}](2.1)$$Магнитная составляющая имеет направление перпендикулярное вектору скорости ($\bar{v}$) и вектору магнитной индукции ($\bar{B}$). Электрическая составляющая сонаправлена с вектором напряжённости ($\bar{E}$) электрического поля. В соответствии со вторым законом Ньютона имеем:
$$\bar{F}=q \bar{E}+q[\bar{v} \times \bar{B}]=m \bar{a}(2.2)$$Получаем, что ускорение равно:
$$\frac{q \bar{E}+q[\bar{v} \times \bar{B}]}{m}=\bar{a}(2.3)$$Если скорость заряда параллельна векторам $\bar{E}$ и $\bar{B}$, тогда $[\bar{v} \times \bar{B}]=0$, получим:
$$\bar{a}=\frac{q \bar{E}}{m}$$Ответ. $\bar{a}=\frac{q \bar{E}}{m}$
Читать дальше: Формула силы натяжения нити.