Формула равноускоренного движения

Задание. Тело было брошено вертикально вверх. Оно возвратилось на землю через промежуток времени, равный t. Какой была начальная скорость тела, и на какую высоту оно поднялось?

Решение. Тело в поле тяжести Земли движется с постоянным ускорением равным ускорению свободного падения, на рис.1 оно направлено вниз.

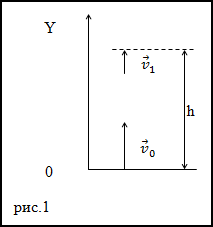
В качестве основы для решения задачи используем формулу для перемещения при равноускоренном движении:

$$\bar{s}=\bar{s}_{0}+\bar{v}_{0} t+\frac{\bar{a} t^{2}}{2}$$

Все движение происходит только по оси Y, поэтому проекция выражения (1.1) примет вид:

$$y(t)=v_{0} t-\frac{g t^{2}}{2}(1.2)$$

Формула для скорости при равноускоренном движении записывается как:

$$\bar{v}=\bar{v}_{0}+\bar{a} t(1.3)$$

В проекции на ось она преобразуется к виду:

$$v(t)=v_{0}-g t(1.4)$$

Точке максимального подъема мы имеем y(t₁)=h и v(t₁)=0 (t₁ - время поъема), тогда выражения (1.2) и (1.4) перепишем как:

$$h=v_{0} t_{1}-\frac{g\left(t_{1}\right)^{2}}{2}, 0=v_{0}-g t_{1}(1.5)$$

где $t_{1}=\frac{t}{2}$ . Следовательно,

$$v_{0}=\frac{g t}{2}(1.6)$$

Подставляя выражение (1.6) вместо начальной скорости в формулу h, имеем:

$$h=\frac{g t}{2} \cdot \frac{t}{2}-\frac{g\left(\frac{t}{2}\right)^{2}}{2}=\frac{g t^{2}}{8}$$

Ответ. $v_{0}=\frac{g t}{2} ; h=\frac{g t^{2}}{8}$

Задание. Расстояние между двумя точками равно l. Первую половину пути тело проходит равноускорено, вторую равнозамедленно. Максимальная скорость тела равна v. Каков модуль ускорения тела и время его перемещения, если ускорения на обоих участках пути равны по модулю.

Решение. Данную задачу можно решить двумя способами.

1 способ аналитический.

В качестве основы для решения задачи используем формулу для перемещения при равноускоренном движении:

$$\bar{s}=\bar{s}_{0}+\bar{v}_{0} t+\frac{\bar{a} t^{2}}{2}(2.1)$$

Для первой половины пути, учитывая, что мы рассматриваем прямолинейное движение, запишем:

$$s=\frac{a t_{1}^{2}}{2}(2.2)$$

где учтено, что $\bar{s}_{0}=0, \bar{v}_{0}=0, s=\frac{l}{2}$ .

Для второй половины пути получаем:

$$s^{\prime}=v t_{2}-\frac{a t_{2}^{2}}{2}(2.3)$$

где $s^{\prime}=\frac{l}{2}$ .

Суммарное время, которое провело тело в пути равно:

$$t=t_{1}+t_{2}(2.4)$$

Наибольшая скорость движения равна:

$$v=a t_{1}=a t_{2} \rightarrow t_{1}=t_{2}(2.5)$$

Суммарный путь равен:

$$l=\frac{a t_{1}^{2}}{2}+v t_{2}-\frac{a t_{2}^{2}}{2} \rightarrow t_{2}=\frac{l}{v}$$

Ускорение выразим из (2.2), имеем:

$$a=\frac{l}{t_{1}^{2}}=\frac{v^{2}}{l}$$

2.графический способ решения задачи.

Для этого построим график зависимости v(t).

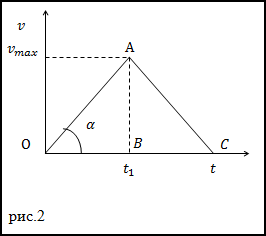
Путь равен площади под кривой или в нашем случае сумме площадей треугольниковOABи ABC. Значит можно записать:

$$ \begin{array}{c} l=\frac{v_{\max } t_{1}}{2}+\frac{v_{\max } t_{2}}{2} \rightarrow t=\frac{2 l}{v_{\max }}=\frac{2 l}{v} \\ a=\operatorname{tg} \alpha=\frac{v_{\max }}{t / 2}=\frac{v^{2}}{l} \end{array} $$

Ответ. $t=\frac{2 l}{v}, a=\frac{v^{2}}{l}$