Содержание:

Определение и формула количества теплоты

Внутреннюю энергию термодинамической системы можно изменить двумя способами:

  1. совершая над системой работу,
  2. при помощи теплового взаимодействия.

Передача тепла телу не связана с совершением над телом макроскопической работы. В данном случае изменение внутренней энергии вызвано тем, что отдельные молекулы тела с большей температурой совершают работу над некоторыми молекулами тела, которое имеет меньшую температуру. В этом случае тепловое взаимодействие реализуется за счет теплопроводности. Передача энергии также возможна при помощи излучения. Система микроскопических процессов (относящихся не ко всему телу, а к отдельным молекулам) называется теплопередачей. Количество энергии, которое передается от одного тела к другому в результате теплопередачи, определяется количеством теплоты, которое предано от одного тела другому.

Определение

Теплотой называют энергию, которая получается (или отдается) телом в процессе теплообмена с окружающими телами (средой). Обозначается теплота, обычно буквой Q.

Это одна из основных величин в термодинамике. Теплота включена в математические выражения первого и второго начал термодинамики. Говорят, что теплота – это энергия в форме молекулярного движения.

Теплота может сообщаться системе (телу), а может забираться от нее. Считают, что если тепло сообщается системе, то оно положительно.

Формула расчета теплоты при изменении температуры

Элементарное количество теплоты обозначим как $\delta Q$. Обратим внимание, что элемент тепла, которое получает (отдает) система при малом изменении ее состояния не является полным дифференциалом. Причина этого состоит в том, что теплота является функцией процесса изменения состояния системы.

Элементарное количество тепла, которое сообщается системе, и температура при этом меняется от Tдо T+dT, равно:

$$\delta Q=C d T(1)$$

где C – теплоемкость тела. Если рассматриваемое тело однородно, то формулу (1) для количества теплоты можно представить как:

$$\delta Q=c m d T=\nu c_{\mu} d T(2)$$

где $c=\frac{C}{m}$ – удельная теплоемкость тела, m – масса тела, $c_{\mu}=c \cdot \mu$ - молярная теплоемкость, $\mu$ – молярная масса вещества, $\nu=\frac{m}{\mu}$ – число молей вещества.

Если тело однородно, а теплоемкость считают независимой от температуры, то количество теплоты ($\Delta Q$), которое получает тело при увеличении его температуры на величину $\Delta t = t_2 - t_1$ можно вычислить как:

$$\Delta Q=c m \Delta t(3)$$

где t2, t1 температуры тела до нагрева и после. Обратите внимание, что температуры при нахождении разности ($\Delta t$) в расчетах можно подставлять как в градусах Цельсия, так и в кельвинах.

Формула количества теплоты при фазовых переходах

Переход от одной фазы вещества в другую сопровождается поглощением или выделением некоторого количества теплоты, которая носит название теплоты фазового перехода.

Так, для перевода элемента вещества из состояния твердого тела в жидкость ему следует сообщить количество теплоты ($\delta Q$) равное:

$$\delta Q=\lambda d m$$

где $\lambda$ – удельная теплота плавления, dm – элемент массы тела. При этом следует учесть, что тело должно иметь температуру, равную температуре плавления рассматриваемого вещества. При кристаллизации происходит выделение тепла равного (4).

Количество теплоты (теплота испарения), которое необходимо для перевода жидкости в пар можно найти как:

$$\delta Q=r d m$$

где r – удельная теплота испарения. При конденсации пара теплота выделяется. Теплота испарения равна теплоте конденсации одинаковых масс вещества.

Единицы измерения количества теплоты

Основной единицей измерения количества теплоты в системе СИ является: [Q]=Дж

Внесистемная единица теплоты, которая часто встречается в технических расчетах. [Q]=кал (калория). 1 кал=4,1868 Дж.

Примеры решения задач

Пример

Задание. Какие объемы воды следует смешать, чтобы получить 200 л воды при температуре t=40С, если температура одной массы воды t1=10С, второй массы воды t2=60С?

Решение. Запишем уравнение теплового баланса в виде:

$$Q=Q_{1}+Q_{2}(1.1)$$

где Q=cmt – количество теплоты приготовленной после смешивания воды; Q1=cm1t1 - количество теплоты части воды температурой t1 и массой m1; Q2=cm2t2- количество теплоты части воды температурой t2 и массой m2.

Из уравнения (1.1) следует:

$$ \begin{array}{l} \mathrm{cmt}=\mathrm{cm}_{1} t_{1}+\mathrm{~cm}_{2} t_{2} \rightarrow \mathrm{mt}=\mathrm{m}_{1} t_{1}+\mathrm{~m}_{2} t_{2} \rightarrow \\ \rightarrow \rho \mathrm{Vt}=\rho V_{1} t_{1}+\rho \mathrm{V}_{2} t_{2} \rightarrow \mathrm{Vt}=V_{1} t_{1}+V_{2} t_{2}(1.2) \end{array} $$

При объединении холодной (V1) и горячей (V2) частей воды в единый объем (V) можно принять то, что:

$$$ V=V_{1}+V_{2}(1.3) $$$

Так, мы получаем систему уравнений:

$$ \left\{\begin{array}{c} V t=V_{1} t_{1}+V_{2} t_{2} \\ V=V_{1}+V_{2} \end{array}\right. $$

Решив ее получим:

$$ \begin{array}{l} V_{1}=\frac{\left(t_{2}-t\right)}{t_{2}-t_{1}} V \\ V_{2}=\frac{\left(t-t_{1}\right)}{t_{2}-t_{1}} V \end{array} $$

Проведем вычисления (это можно сделать, не переходя в систему СИ):

$$ \begin{array}{l} V_{1}=\frac{(60-40)}{60-10} 200=80 \text { (л) } \\ V_{2}=\frac{(40-10)}{60-10} 200=120 \text { (л) } \end{array} $$

Ответ. V1=80 л, V2=120 л.


Warning: file_put_contents(./students_count.txt): failed to open stream: Permission denied in /var/www/webmath-q2ws/data/www/webmath.ru/poleznoe/guide_content_banner.php on line 20
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 471 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

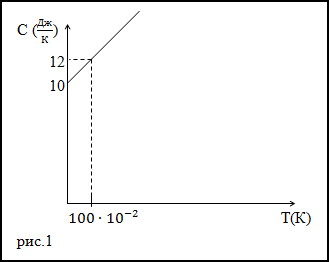
Задание. Теплоемкость тела изменяется по линейному закону (рис.1) в зависимости от абсолютной температуры в рассматриваемом интервале $T_{1} \leq T \leq T_{2}$ . Какое количество теплоты получает тело, если T1=300 К, T2=400 К.

Решение. Исследуя график функции теплоемкости (C(T)) (рис.1) запишем его аналитическое выражение, оно получится:

$C(T)=10+2 \cdot 10^{-2} T$ (Дж/К)

Основой для решения задачи послужит формула для количества теплоты в виде:

$$\delta Q=C d T(2.2)$$

Подставим полученное выражение для теплоемкости (2.1) в формулу (2.2) поведем интегрирование в заданном интервале температур:

$$ \begin{array}{c} \Delta Q=\int_{300}^{400}\left(10+2 \cdot 10^{-2} T\right) d T=\left.\left(10 \cdot T+10^{-2} T^{2}\right)\right|_{300} ^{400}= \\ =\left(10 \cdot 400+10^{-2} \cdot(400)^{2}\right)-\left(10 \cdot 300+10^{-2} \cdot(300)^{2}\right)=1700\left(\mathrm{~A}^{*}\right) \end{array} $$

Ответ. $\Delta Q$=1700 Дж


Читать дальше: Формула напряженности магнитного поля.