Напряженностью магнитного поля $\bar{H}$ называют векторную физическую величину, направленную по касательной к силовым линиям поля, являющуюся характеристикой магнитного поля, равную:
$$\bar{H}=\frac{\bar{B}}{\mu_{0}}-\bar{J}(1)$$Содержание:
- Определение и формула напряженности магнитного поля
- Закон Био-Савара-Лапласа
- Единицы измерения
- Примеры решения задач
Определение и формула напряженности магнитного поля
Определение
где $\bar{B}$ – вектор магнитной индукции, $\mu_{0}=4 \pi \cdot 10^{-7}$ Гн/м(Н/А2)- магнитная постоянная, $\bar{j}$ – вектор намагниченности среды в исследуемой точке поля.
Для магнитного поля в вакууме напряженность магнитного поля определяется выражением:
$$\bar{H}=\frac{\bar{B}}{\mu_{0}}$$В изотропной среде формула (1) преобразуется к виду:
$$\bar{H}=\frac{\bar{B}}{\mu_{0} \mu}$$где $\mu$ – скалярная величина, называемая относительной магнитной проницаемостью среды (или просто магнитной проницаемостью). В изотропной среде векторы напряженности магнитного поля и магнитной индукции совпадают по направлению.
Иногда напряженность магнитного поля $d \bar{H}$ определяют как векторную величину, направленную по касательной к силовой линии поля, по модулю равной отношению силы (dF), с которой поле воздействует на единичный элемент тока (dl), который расположен перпендикулярно полю в вакууме, к магнитной постоянной:
$$d H=\frac{d F}{\mu_{0} I d l}$$Закон Био-Савара-Лапласа
Это важнейший в электромагнетизме закон. Он определяет вектор напряженности $d \bar{H}$ в произвольной точке магнитного поля, которое создает в вакууме элементарный проводник длинны dl с постоянным током I:
$$d \bar{H}=\frac{1}{4 \pi} \frac{I}{r^{3}} d \bar{l} \times \bar{r}(5)$$где $d \bar{l}$ – вектор элемента проводника, который по модулю равен длине проводника, направление совпадает с направлением тока; $\bar{r}$ – радиус–вектор, который проводят от рассматриваемого элементарного проводника к точке рассмотрения поля; $r=|\bar{r}|$ .
Вектор $d \bar{H}$ – перпендикулярен плоскости, в которой находятся векторы $d \bar{l}$ и $\bar{r}$, и направлен так, что из его конца вращение вектора $d \bar{l}$ по кратчайшему пути до совмещения с вектором $\bar{r}$ происходило по часовой стрелке. Для нахождения направления вектора $d \bar{H}$ можно использовать правило буравчика (Буравчик (винт) вращаем так, чтобы его поступательное движение совпадало с направлением тока, тогда направление, по которому вращается ручка винта, совпадает с направлением вектора напряженности поля, которое создает рассматриваемый ток).
Закон Био-Савара-Лапласа дает возможность вычислять величину полной напряженности магнитного поля, которое создает ток, текущий по проводнику любой формы.
Для нахождения полной напряженности магнитного поля, которое создает в исследуемой точке ток I, который течет по проводнику l, следует векторно суммировать все элементарные напряженности $d \bar{H}$, порождаемые элементами проводника и найденные по формуле (4).
Единицы измерения
Основной единицей измерения момента силы в системе СИ является: [H]=А/м
Примеры решения задач
Пример
Задание. Чему равна напряженность (H) в центре кругового витка (R - радиус витка) с током I.
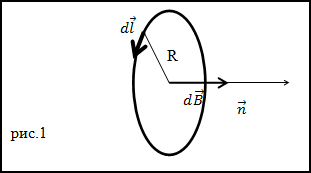
Решение. Каждый элементарный ток витка магнитное поле в центре окружности, напряженность которого направлена по положительной нормали к плоскости контура витка (рис.1). Поэтому, если элементарную напряженность поля найти по закону Био-Савара – Лапласа, то векторное сложение элементарных полей можно будет заменить на алгебраическое.
В соответствии с законом Био-Савара – Лапласа dH равно:
$$d \bar{H}=\frac{1}{4 \pi} \frac{I}{r^{3}} d \bar{l} \times \bar{r}(1.1)$$Применяя выражение (1.1) к нашему случаю, получим:
$$d H=\frac{1}{4 \pi} \frac{I d l}{R^{2}}(1.2)$$Возьмем интеграл по контуру, получим:
$$H=\oint_{L} \frac{1}{4 \pi} \frac{I d l}{R^{2}}=\frac{1}{4 \pi} I \cdot \frac{2 \pi R}{R^{2}}=\frac{I}{2 R}$$Ответ. $H=\frac{I}{2 R}$
Warning: file_put_contents(./students_count.txt): failed to open stream: Permission denied in /var/www/webmath-q2ws/data/www/webmath.ru/poleznoe/guide_content_banner.php on line 20
Пример
Задание. Какова напряженность магнитного поля, которую создает электрон, движущийся прямолинейно и равномерно со скоростью v? Если точка, в которой исследуется поле, находится на расстоянии r от электрона на перпендикуляре к вектору скорости, если перпендикуляр провести через мгновенное положение частицы.
Решение. Сделаем рисунок.
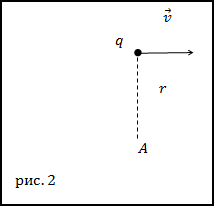
Напряженность магнитного поля будем искать, применяя закон Био – Савара – Лапласа:
$$d \bar{H}=\frac{1}{4 \pi} \frac{I}{r^{3}} d \bar{l} \times \bar{r}(2.1)$$Учтем, что:
$$I d l=S j d l(2.2)$$Если все заряды одинаковы (q), то плотность тока равна:
$$\bar{j}=q n \bar{v}(2.3)$$заряд отрицательный, следовательно, направления векторов $\bar{j}$ и $\bar{v}$ противоположны. n – концентрация зарядов. Подставим формулу (2.3) в (2.2), результат в (2.1) получаем:
$$d \bar{H}=\frac{1}{4 \pi} \frac{S q n d l}{r^{3}} \bar{v} \times \bar{r}(2.4)$$где dN=Sdln - количество заряженных частиц в отрезке dl. В таком случае, напряженность поля, которое создает один заряд:
$$\bar{H}=\frac{d \bar{H}}{d N}=\frac{1}{4 \pi} \frac{q}{r^{3}} \bar{v} \times \bar{r}(2.4)$$По условию задачи $\bar{v} \perp \bar{r}$ , значит модуль напряжённости магнитного поля в точке А (рис.2) будет равен:
$$H=\frac{1}{4 \pi} \frac{q v}{r^{2}}$$Ответ. $H=\frac{1}{4 \pi} \frac{q v}{r^{2}}$
Читать дальше: Формула напряженности электрического поля.
Статьи по теме
Поможем выполнить
любую работу
