Длиной волны называют кратчайшее пространственное расстояние между ее точками, совершающими колебания в одной фазе. Обозначают длину волны, чаще всего буквой $\lambda$ .
Содержание:
- Определение и формула длины волны
- Длина стоячей волны
- Длина бегущей волны
- Длина бегущей волны
- Длина электромагнитной волны
- Единицы измерения длины волны
- Примеры решения задач
Определение и формула длины волны
Определение
Для синусоидальных волн $\lambda$ – это расстояние, на которое волна распространяется за один период (T). Длину волны в этом случае еще называют пространственным периодом. Тогда формулой длины волны можно считать выражение:
$$\lambda=v T=\frac{v}{\nu}=\frac{2 \pi}{k}$$где v – скорость распространения волны, $\nu=\frac{1}{T}$ – частота колебаний, $k=\frac{\omega}{v}$ – волновое число, $T=\frac{2 \pi}{\omega}$ – период волны, $\omega$ – циклическая частота волны.
Длина стоячей волны
Длиной стоячей волны($\lambda_{st}$) называют расстояние в пространстве между двумя пучностями (или узлами):
$$\lambda_{s t}=\frac{\pi}{k}=\frac{\lambda}{2}(2)$$где $\lambda$ – длина бегущей волны. Надо заметить, что расстояние между соседними пучностью и узлом связывает равенство:
$$\frac{\lambda_{s t}}{2}=\frac{\lambda}{4}(3)$$Длина бегущей волны
В бегущей волне длина волны связана с фазовой скоростью (vph) формулой:
$$\lambda=\frac{v_{p h}}{\nu}(4)$$Длина бегущей волны
Разность фаз и длина волны
Две точки волны находящиеся на расстоянии $\Delta x$ имеют при колебании разность фаз ($\Delta \varphi$), которая равна:
$$\Delta \varphi=\frac{2 \pi \Delta x}{\lambda}(5)$$Длина электромагнитной волны
Скорость распространения электромагнитных волн в вакууме равна скорости света в вакууме ($c \approx 3 \cdot 10^{8}$ м/с), следовательно, длина электромагнитной волны в вакууме, может быть рассчитана при помощи формулы:
$$\lambda=c T=\frac{c}{\nu}(6)$$Длина электромагнитной волны в веществе равна:
$$\lambda=\frac{c}{n \nu}(7)$$где $n=\sqrt{\varepsilon \mu}$ – показатель преломления вещества, $\varepsilon$ – диэлектрическая проницаемость вещества, $\mu$ – магнитная проницаемость вещества.
Отметим, что все рассматриваемые формулы относят к случаю T=const.
Единицы измерения длины волны
Основной единицей измерения длины волны в системе СИ является: [$\lambda$]=м
В СГС: [$\lambda$]=см
Примеры решения задач
Пример
Задание. Каково приращение длины электромагнитной волны, имеющей частоту v=1 МГц при ее переходе в немагнитную среду, которая имеет диэлектрическую проницаемость $\varepsilon$=2?
Решение. Так как речь в условии задачи идет о немагнитной среде, в которую переходит волна, то считаем магнитную проницаемость вещества равной единице ($\mu$=1).
Длина рассматриваемой нами волны в вакууме равна:
$$\lambda_{1}=\frac{c}{\nu}(1.1)$$Длина волны в веществе:
$$\lambda_{2}=\frac{c}{n \nu}=\frac{c}{\sqrt{\varepsilon \mu} \cdot \nu}(1.2)$$Используя выражения (1.1) и (1.2) найдем изменение длины волны:
$$\Delta \lambda=\lambda_{2}-\lambda_{1}=\frac{c}{\sqrt{\varepsilon \mu} \cdot \nu}-\frac{c}{\nu}=\frac{c}{\nu}\left(\frac{1}{\sqrt{\varepsilon \mu}}-1\right)$$Проведем вычисления, если нам известно помимо данных приведенных в условии задачи, что $c \approx 3 \cdot 10^{8}$ м/с- скорость света в вакууме, и v=1 МГц=106 Гц:
$$\Delta \lambda=\frac{3 \cdot 10^{8}}{10^{6}}\left(\frac{1}{\sqrt{4 \cdot 1}}-1\right)=-1,5 \cdot 10^{2}(\mathrm{~m})$$Ответ. Длина волны уменьшится на 150 м
Пример
Задание. Какова длина плоской синусоидальной волны, которая распространяется по оси X. Две точки, которые находятся на оси X расположенные на расстояниях 2 м и 3 м от источника совершают колебания с разностью фаз равной $\Delta \varphi=\frac{3 \pi}{5}$ . Каким будет период колебаний в волне, если ее скорость в данной среде равна v=2м/с?
Решение. Сделаем рисунок.
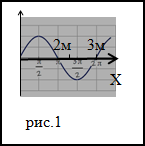
Основой для решения задачи будет формула:
$$\Delta \varphi=\frac{2 \pi \Delta x}{\lambda}=\frac{2 \pi\left(x_{2}-x_{1}\right)}{\lambda}(2.1)$$Выразим из (2.1) искомую длину волны, получим:
$$\lambda=\frac{2 \pi\left(x_{2}-x_{1}\right)}{\Delta \varphi}(2.2)$$Период колебаний связан с длиной волны формулой:
$$T=\frac{\lambda}{v}(2.3)$$C учетом (2.2), имеем:
$$T=\frac{2 \pi\left(x_{2}-x_{1}\right)}{\Delta \varphi v}$$Проведем вычисления:
$$ \begin{array}{c} \lambda=\frac{2 \pi(3-2)}{3 \pi} \cdot 5=\frac{10}{3}(m) \\ T=\frac{10}{3 \cdot 2}=1,67(c) \end{array} $$Ответ. $\lambda \approx 3,3 \mathrm{~m} ; T \approx 1,67 \mathrm{c}$
Читать дальше: Формула количества теплоты.










