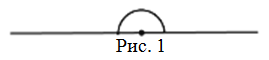
Развернутый угол - это угол, стороны которого составляют прямую (рис. 1).
Градусная мера развернутого угла равна $180^{\circ}$.
Содержание:
Определение
Развернутый угол - это угол, стороны которого составляют прямую (рис. 1).
Градусная мера развернутого угла равна $180^{\circ}$.
Любой луч, проведенный из вершины развернутого угла, делит его на два угла. Полученные в результате углы имеют одну общую сторону, а две другие составляют прямую. Такие углы называются смежными.
Биссектриса развернутого угла делит его на два прямых угла.
Если произвольный луч, проведенный из вершины развернутого угла, не является биссектрисой, то он делит развернутый угол на два, один из которых острый (меньше прямого), а другой - тупой (больше прямого)
Пример
Задание. Развернутый угол разделен лучом на два угла, градусные меры которых относятся как 1:4. Найдите полученные углы.
Решение. Обозначим искомые углы как $\alpha$ и $\beta$ . Пусть $x$ - коэффициент пропорциональности, тогда $\alpha = x$, а соответственно $\beta = 4x$ . Так как градусная мера развернутого угла равна $180^{\circ}$ и согласно свойствам угла, что градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами, то делаем вывод, что
$$x+4 x=180^{\circ} \Rightarrow 5 x=180^{\circ}$$Отсюда находим:
$x=\alpha=36^{\circ}$ и $\beta=4 x=4 \cdot 36^{\circ}=144^{\circ}$
Ответ. $36^{\circ}$ и $144^{\circ}$
Пример
Задание. Луч $OC$ делит развернутый угол $AOB$ на два угла $AOC$ и $BOC$ так, что угол $AOC$ на $30^{\circ}$ больше угла $BOC$ . Найти углы $AOC$ и $BOC$ .
Решение. Изобразим заданный развернутый угол и проведем луч $OC$ (рис. 2).
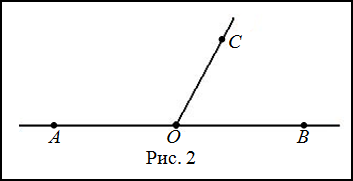
Пусть $\angle B O C=x^{\circ}$, тогда из условия получаем, что $\angle A O C=(x+30)^{\circ}$. Так как эти углы являются смежными, то их сумма равна $180^{\circ}$, то есть
$$\angle A O C+\angle B O C=180^{\circ}$$а тогда
$$x+x+30=180 \Rightarrow 2 x=150 \Rightarrow x^{\circ}=\angle B O C=75^{\circ}$$Отсюда
$$\angle A O C=(x+30)^{\circ}=105^{\circ}$$Ответ. $\angle A O C=105^{\circ}, \angle B O C=75^{\circ}$
Читать дальше: что такое вертикальные углы.