Содержание:

Определение биссектрисы

Определение

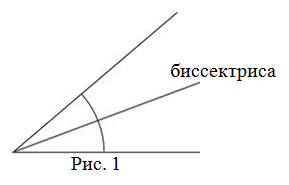
Биссектрисой (от лат. bi - "двойное", и sectio - "разрезание") угла называется луч, который исходит из вершины угла и делить угол на две равные части (пополам) (рис. 1).

Мнемоническое правило: биссектриса это крыса, которая бегает по углам и делит угол пополам.

Пример

Задание. В угле $\alpha=150^{\circ}$ проведена биссектриса. Чему равен каждый из полученных углов?

Решение. Так как по определению биссектриса делит угол на два равных, то полученные углы равны соответственно

$$\angle \alpha_{1}=\angle \alpha_{2}=\frac{150^{\circ}}{2}=75^{\circ}$$

Ответ. 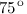и $75^{\circ}$ и $75^{\circ}$

Свойства биссектрис

  1. Теорема (Свойство биссектрисы). Биссектриса внутреннего угла треугольника делит противоположную сторону в отношении, равном отношению двух прилежащих сторон (рис. 2):

    $$\frac{x}{y} = \frac{a}{b}$$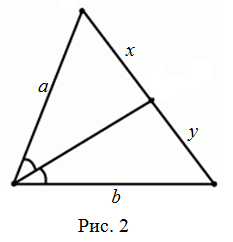

  2. Биссектрисы внутренних углов треугольника пересекаются в одной точке, называемой инцентром, в центре вписанной в этот треугольник окружности.
  3. Биссектрисы одного внутреннего и двух внешних углов треугольника пересекаются в одной точке. Эта точка является центром одной из трех вневписанных окружностей этого треугольника.
  4. Основания биссектрис двух внутренних и одного внешнего углов треугольника лежат на одной прямой, если биссектриса внешнего угла не параллельна противоположной стороне треугольника.
  5. Если биссектрисы внешних углов треугольника не параллельны противоположным сторонам, то их основания лежат на одной прямой.

  6. Теорема Штейнера-Лемуса. Если в треугольнике две биссектрисы равны, то треугольник - равнобедренный.

    Якоб Штейнер (1796 - 1863) - швейцарский математик, основатель синтетической геометрии кривых линий и поверхностей 2-го и высших порядков. Даниель Христиан Лудольф Лемус (1780 - 1863) - французский математик.

  7. Построение треугольника по трем заданным биссектрисам с помощью циркуля и линейки невозможно, причём даже при наличии трисектора.
  8. В равнобедренном треугольнике биссектриса угла, противоположного основанию, является медианой и высотой.

  9. Расстояния от сторон угла до любой точки биссектрисы одинаковы.

    Если задан треугольник со сторонами $a$, $b$ и $c$, то длина биссектрисы, проведенной к стороне $c$, вычисляется по формуле:

    $$l_{c}=\frac{\sqrt{a b(a+b+c)(a+b-c)}}{a+b}$$

Warning: file_put_contents(./students_count.txt): failed to open stream: Permission denied in /var/www/webmath-q2ws/data/www/webmath.ru/poleznoe/guide_content_banner.php on line 20
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 452 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. В треугольнике $ABC$ проведена биссектриса $AD$. Найти периметр треугольника, если $AC=4$, $DC=2$ и $BD=3$.

Решение. Сделаем чертеж (рис. 3).

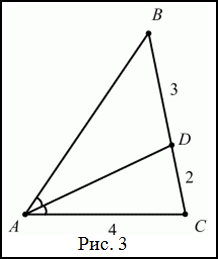
По теореме про свойство биссектрисы имеем:

$$\frac{B D}{D C}=\frac{A B}{A C} \Rightarrow \frac{3}{2}=\frac{A B}{4} \Rightarrow A B=\frac{3 \cdot 4}{2}=6$$

А тогда периметр треугольника, как сумма всех сторон, равен:

$$P_{\Delta A B C}=6+3+2+4=15$$

Ответ. $P_{\Delta A B C}=15$

Читать дальше: что такое вершина угла.