Смежными углами называются два прилежащих угла, несовпадающие стороны которых образуют прямую (рис. 1).
Содержание:
- Определение смежных углов
- Следствия из теоремы о смежных углах
- Свойства (тригонометрические соотношения)
Определение смежных углов
Определение
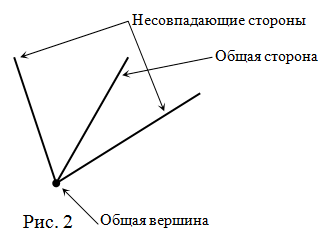
Определение
Теорема
Теорема о смежных углах.
Сумма градусных мер смежных углов равна $180^{\circ}$.
Пример
Задание. Чему равна градусная мера угла $\alpha$, если градусная мера смежного с ним угла равна $70^{\circ}$?
Решение. Из теоремы о смежных углах получаем, что
$$\alpha+70^{\circ}=180^{\circ}$$Отсюда $\alpha=180^{\circ}-70^{\circ}=110^{\circ}$
Ответ. $\alpha=110^{\circ}$
Следствия из теоремы о смежных углах
- Если два угла равны, то углы, которые являются для них смежными, также равны.
- Если угол не развернутый, то он не равен 180 градусам.
- Угол, который является смежным прямому углу (то есть углу, градусная мера которого равна $90^{\circ}$), также является прямым.
- Угол, смежный с острым углом (величина которого меньше $90^{\circ}$), является тупым (величина больше $90^{\circ}$), а смежный тупому - острым.
Пример
Задание. Доказать, что для двух неравных углов, их смежные углы также не равны, причем большему углу соответствует меньший смежный угол.
Доказательство. Пусть заданы два угла $\angle \alpha \neq \angle \beta$. Для определенности будем считать, что $\angle \alpha > \angle \beta$. Пусть $\angle \alpha_{1}$ и $\angle \beta_{1}$ - соответствующие им смежные углы. Тогда по теореме о смежных углах имеем:
$$\angle \alpha_{1}=180^{\circ}-\angle \alpha, \angle \beta_{1}=180^{\circ}-\angle \beta$$Так как $\angle \alpha \neq \angle \beta$, то и разности, стоящие в правых частях последних равенств также не равны, причем при равенстве уменьшаемого та разность меньше, где вычитаемое больше, следовательно $\angle \alpha_{1} < \angle \beta_{1}$.
Что и требовалось доказать.
Свойства (тригонометрические соотношения)
- Синусы смежных углов равны. Их косинусы и тангенсы равны по величине, но имеют противоположные знаки (за исключением неопределённых значений).
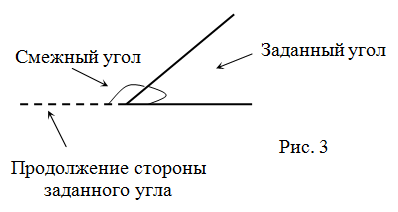
- Чтобы построить угол, смежный данному, надо одну из сторон рассматриваемого угла продлить за вершину (рис. 3).
Читать дальше: что такое острый угол.










