Содержание:

Определения

Определение

Периметр - общая длина границы фигуры, которая чаще всего находится на плоскости.

Периметр имеет ту же размерность величин, что и длина. Иногда периметром называют границу геометрической фигуры. Чаще всего этот термин применяется к треугольнику и многоугольникам и в этом случае означает сумму длин всех сторон фигуры. То есть периметр - это сумма длин сторон какой-либо геометрической фигуры.

Определение

Полупериметр - половина периметра. Употребляется в основном в геометрии треугольника.

Формулы периметра основных геометрических фигур

Периметр треугольника

Чтобы найти периметр треугольника $ABC$, необходимо сложить длины всех его сторон.

$$P_{\Delta A B C}=a+b+c$$

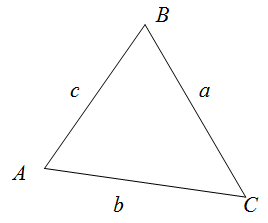
Читать дальше: формула периметра треугольника и примеры решений →

Периметр круга

Чтобы найти периметр круга, необходимо вычислить длину окружности, которая его ограничивает.

Для нахождения длины окружности можно использовать одну из формул

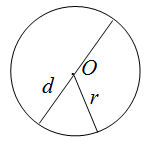
Читать дальше: формула периметра круга и примеры решений →


Периметр квадрата

Чтобы найти периметр квадрата, необходимо длину его стороны умножить на четыре.

$$P_{\Delta A B C D}=a+a+a+a=4 a$$

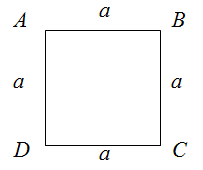
Читать дальше: формула периметра квадрата и примеры решений →


Периметр прямоугольника

Чтобы найти периметр прямоугольника, нужно сумму его ширины и длины умножить на два.

$$P_{\Delta A B C D}=a+b+a+b=2 a+2 b=2(a+b)$$

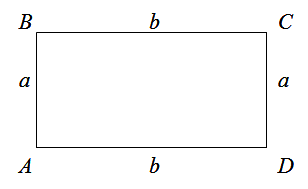
Читать дальше: формула периметра прямоугольника и примеры решений →


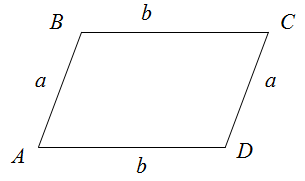
Периметр параллелограмма

Чтобы найти периметр параллелограмма, нужно сумму двух непараллельных сторон умножить на два.

$$P_{\Delta A B C D}=a+b+a+b=2 a+2 b=2(a+b)$$

Читать дальше: формула периметра параллелограмма и примеры решений →

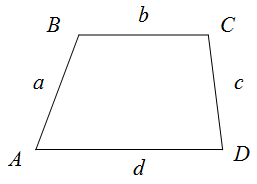
Периметр трапеции

Чтобы найти периметр трапеции необходимо найти сумму длин её сторон.

$$P_{\Delta A B C D}=a+b+c+d$$

Читать дальше: формула периметра трапеции и примеры решений →


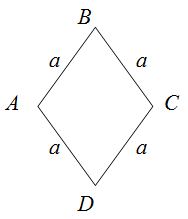
Периметр ромба

Чтобы найти периметр ромба, необходимо длину его стороны умножить на четыре.

$$P_{\Delta A B C D}=a+a+a+a=4 a$$

Читать дальше: формула периметра ромба и примеры решений →


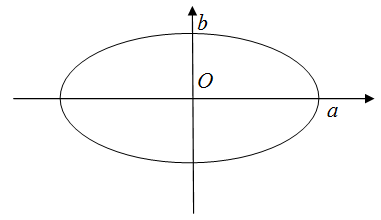
Периметр эллипса

Чтобы найти периметр эллипса $\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$, нужно воспользоваться формулой

$$P=4 \cdot \frac{\pi a b+(a-b)}{a+b}$$

Читать дальше: формула периметра эллипса и примеры решений →