Содержание:

Формула

Чтобы найти периметр трапеции необходимо найти сумму длин её сторон.

В общем случае для произвольной трапеции $ABCD$ со сторонами $AB=a$, $BC=b$, $CD=c$, $AD=d$ периметр вычисляется по формуле:

$$P_{\Delta A B C D}=a+b+c+d$$

Если трапеция $ABCD$ равнобокая, то по определению её боковые стороны равны $AB=CD=a$ и формула для нахождения периметра примет вид:

$$P_{\Delta A B C D}=2 a+b+d$$

Примеры вычисления периметра трапеции

Пример

Задание. Найти периметр трапеции $ABCD$ со сторонами $AB=1,5$ см, $BC=2$ см, $CD=1$ см, $AD=3$ см.

Решение. Для нахождения периметра трапеции $ABCD$ воспользуемся формулой

$$P_{\Delta A B C D}=A B+B C+C D+A D$$

Подставляя в неё заданные в условии длины сторон, получим:

$P_{\Delta A B C D}=1,5+2+1+3=7,5$ (см)

Ответ. $P_{\Delta A B C D}=7,5$ (см)

Все формулы периметров Калькулятор периметра трапеции

Warning: file_put_contents(./students_count.txt): failed to open stream: Permission denied in /var/www/webmath-q2ws/data/www/webmath.ru/poleznoe/guide_content_banner.php on line 20
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 456 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Заданна равнобокая трапеция $ABCD$ с основаниями $BC=3$ см, $AD=7$ см и высотой $BK=2 \sqrt{3}$ см. Найти периметр заданной трапеции.

Решение. Сделаем рисунок.

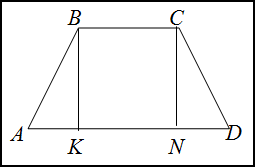
Опустим высоту $CN$. Полученный в результате четырехугольник $BCKN$ является прямоугольником, поэтому $BC=KN$. Треугольники $\Delta A B K \quad$ и $\quad \Delta N C D$ - прямоугольные и равны между собой. Тогда $AK=ND$. Найдем чему равно $AK$:

$A K=(A D-B C): 2 \Rightarrow A K=(7-3): 2=2$ (см)

Из $\Delta ABK$ по теореме Пифагора найдем боковую сторону $AB$ трапеции:

$=\sqrt{12+4}=\sqrt{16}=4$ (см)

Тогда периметр рассматриваемой равнобокой трапеции

$P_{\Delta A B C D}=2 \cdot 4+3+7=18$ (см)

Ответ. $P_{\Delta A B C D}=18$ (см)

Читать дальше: как найти периметр ромба.