Содержание:

Формула

Чтобы найти периметр ромба, необходимо длину его стороны умножить на четыре.

По определению ромб - это параллелограмм, у которого все стороны равны. Таким образом, формула для нахождения периметра ромба $ABCD$ со стороной $a$ имеет вид:

$$P_{\Delta A B C D}=a+a+a+a=4 a$$

Примеры вычисления периметра ромба

Пример

Задание. Найти периметр ромба $ABCD$ со стороной $a=2,5$ дм.

Решение. Для нахождения периметра ромба $ABCD$ воспользуемся формулой:

$$P_{\Delta A B C D}=4 a$$

Подставляя в неё $a=2,5$ дм, получим:

$P_{\Delta A B C D}=4 \cdot 2,5=10$ (дм)

Ответ. $P_{\Delta A B C D}=10$ (дм)

Все формулы периметров Калькулятор периметра ромба

Warning: file_put_contents(./students_count.txt): failed to open stream: Permission denied in /var/www/webmath-q2ws/data/www/webmath.ru/poleznoe/guide_content_banner.php on line 20
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 453 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

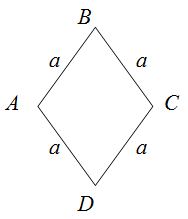
Задание. Найти периметр ромба $ABCD$, если его диагонали равны соответственно $AC=6$ м и $BD=8$ м.

Решение. Сделаем рисунок.

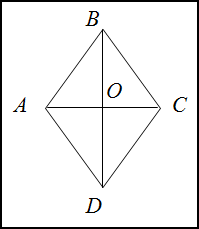
Обозначим $O$ точку пересечения диагоналей. По свойству ромба его диагонали пересекаются под прямым углом и в точке пересечения делятся пополам. Рассмотрим треугольник $ABO$. Он прямоугольный $\angle 0=90^{\circ}$. Его катеты $A O=\frac{A C}{2}=6: 2=3$ (м) и $B O=\frac{B D}{2}=8: 2=4$ (м). Тогда по теореме Пифагора сторона $AC$ равна:

$A C=\sqrt{A O^{2}+B O^{2}}=\sqrt{3^{2}+4^{2}}=\sqrt{9+16}=\sqrt{25}=5$ (м)

Искомый периметр

$P_{\Delta A B C D}=4 \cdot 5=20$ (м)

Ответ. $P_{\Delta A B C D}=20$ (м)

Читать дальше: как найти периметр эллипса.