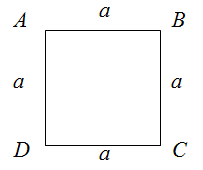Содержание:

Формула

Чтобы найти периметр квадрата, необходимо длину его стороны умножить на четыре.

По определению, квадрат - это правильный четырехугольник, у которого все углы и стороны равны. Тогда, если задан квадрат $ABCD$ со стороной $a$, то для него формула для нахождения периметра примет вид:

$$P_{\Delta A B C D}=a+a+a+a=4 a$$

Примеры вычисления периметра квадрата

Пример

Задание. Дан квадрат $ABCD$ со стороной $a=0,25$ см. Вычислить периметр заданного квадрата.

Решение. Для нахождения периметра квадрата воспользуемся формулой

$$P_{\Delta A B C D}=4a$$

Подставляя в неё значение 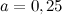, получим:

$P_{\Delta A B C D}=4 \cdot 0,25=1$ (см)

Ответ. $P_{\Delta A B C D}=1$ (см)

Все формулы периметров Калькулятор периметра квадрата

Warning: file_put_contents(./students_count.txt): failed to open stream: Permission denied in /var/www/webmath-q2ws/data/www/webmath.ru/poleznoe/guide_content_banner.php on line 20
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 468 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Найти периметр квадрата $ABCD$, который вписан в окружность радиуса $r=2$ дм.

Решение. Сделаем рисунок.

Диаметр описанной окружности является диагональю вписанного в неё квадрата, то есть

$DB=d=2r=2 \cdot 2=4$ (дм)

Известно, что сторона квадрата $AB$ связана с его диагональю $DB$ соотношением:

$$D B=A B \sqrt{2}$$

Откуда получаем, что

$A B=\frac{D B}{\sqrt{2}}=\frac{4}{\sqrt{2}}=2 \sqrt{2}$ (дм)

А тогда искомый периметр:

Ответ. $P_{\Delta A B C D}=8 \sqrt{2}$ (дм)

Читать дальше: как найти периметр прямоугольника.