Под воздействием силы притяжения к Земле все тела падают с одинаковыми по отношению к ее поверхности ускорениями. Такое ускорение называют ускорением свободного падения и обозначают: g. Его величина в системе СИ считается равной g=9,80665 м/с2 – это так называемое, стандартное значение.
Содержание:
- Определение и формула силы тяжести
- Различие между силой тяжести и силой притяжения к Земле
- Единицы измерения силы тяжести
- Примеры решения задач
Определение и формула силы тяжести
Определение
Вышесказанное обозначает то, что в системе отсчета, которая связывается с Землей, на любое тела обладающее массой m действует сила равная:
$$\bar{P}=m \bar{g}(1)$$которая называется силой тяжести.
Если тело находится в состоянии покоя на поверхности Земли, тогда сила тяжести уравновешивается реакцией подвеса или опоры, которая удерживает тело от падения (вес тела).
Различие между силой тяжести и силой притяжения к Земле
Если быть точным, то следует заметить, что в результате неинерциальности системы отсчета, которая связывается с Землей, сила тяжести отличается от силы притяжения к Земле. Ускорение, которое соответствует движению по орбите существенно меньше, чем ускорение, которое связывается с суточным вращением Земли. Система отсчета, связанная с Землей, осуществляет вращение по отношению к инерциальным системам с угловой скоростью $\omega$=const. Поэтому в случае рассмотрения перемещения тел по отношению к Земле следует учитывать центробежную силу инерции (Fin), равную:
$$F_{i n}=m \omega^{2} r$$где m – масса тела, r – расстояние от оси Земли. Если тело расположено не высоко от поверхности Земли ( в сравнении с радиусом Земли), то можно считать, что
$$r=R_{Z} \cos \varphi(3)$$где RZ – радиус земли, $\varphi$ – широта местности.
В таком случае ускорение свободного падения (g) по отношению к Земле будет определено действием сил: силы притяжения к Земле ( $\bar{F}_{g}$) и силы инерции ( $\bar{F}_{in}$). При этом сила тяжести - есть результирующая этих сил:
$$\bar{P}=\bar{F}_{g}+\bar{F}_{i n}(4)$$Так как сила тяжести сообщает телу, обладающему массой m ускорение равное $\bar{g}$, то соотношение (1) является справедливым.
Разница между силой тяжести $\bar{P}$ и силой притяжения к Земле $\bar{F}_{g}$ небольшая. Так как $F_{g} \gg F_{i n}$.
Как и всякая сила, сила тяжести – векторная величина. Направление силы $\bar{P}$, например, совпадает с направлением нити, натянутой грузом, которое называют направлением отвеса. Сила $\bar{F}_{g}$ направлена к центру Земли. Значит, нить отвеса направлена также только на полюсах и экваторе. На других широтах угол отклонения ($\alpha$) от направления к центру Земли составляет величину, равную:
$$\alpha \approx 0,0018 \sin (2 \varphi)(5)$$Разница между Fg-P максимальна на экваторе, она составляет 0,3% от величины силы Fg. Так как земной шар является сплюснутым около полюсов, то Fg имеет некоторые вариации по широте. Так она у экватора на 0,2% меньше, чем у полюсов. В результате ускорение g изменяется с широтой от 9,780 м/с2 (экватор) до 9,832 м/с2 (полюса).
По отношению к инерциальной системе отсчета (например, гелиоцентрической СО) тело в свободном падении будет перемещаться с ускорением (a) отличающимся от g, равным по модулю:
$$a=\frac{F_{g}}{m}(6)$$и совпадающим по направлению с направлением силы $\bar{F}_{g}$.
Единицы измерения силы тяжести
Основной единицей измерения силы тяжести в системе СИ является: [P]=H
В СГС: [P]=дин
Примеры решения задач
Пример
Задание. Определите во сколько раз величина силы тяжести на Земле (P1) больше, чем сила тяжести на Луне (P2).
Решение. Модуль силы тяжести определяется формулой:
$$P=m g(1.1)$$Если имеется в виду сила тяжести на Земле, то в качестве ускорения свободного падения используем величину $g_{1} \approx 9,8$ м/с^2 . Для вычисления силы тяжести на Луне найдем при помощи справочников ускорение свободного падения на этой планете, оно равно $g_{1} \approx 1,6$ м/с^2 .
$$\frac{P_{1}}{P_{2}}=\frac{m g_{1}}{m g_{2}}=\frac{g_{1}}{g_{2}}$$Таким образом, для ответа на поставленный вопрос следует найти отношение:
$$\frac{P_{1}}{P_{2}}=\frac{9,8}{1,6} \approx 6,1$$Проведем вычисления:
Ответ. $\frac{P_{1}}{P_{2}} \approx 6,1$
Пример
Задание. Получите выражение, которое связывает широту и угол, который образуют вектор силы тяжести и вектор силы притяжения к Земле.
Решение. Угол, который образуется между направлениями силы притяжения к Земле и направлением силы тяжести можно оценить, если рассмотреть рис.1 и применить теорему синусов. На рис.1 изображены: $\bar{F}_{in}$ – центробежная сила инерции, которая возникает за счет вращения Земли вокруг оси, $\bar{P}$ – сила тяжести, $\bar{F}_{g}$ – сила притяжения тела к Земле. Угол $\varphi$ - широта местности на Земле.
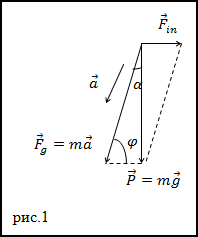
По теореме синусов имеем:
$$\frac{\sin \alpha}{\sin \varphi}=\frac{F_{i n}}{P}(2.1)$$где выражение для центробежной силы можно определить как:
$$F_{i n}=m \omega^{2} R_{Z} \cos \varphi(2.2)$$Rz – радиус Земли. При этом:
$$P=m g(2.3)$$Подставим выражения (2.2) и (2.3) в (2.1), имеем:
$$\frac{\sin \alpha}{\sin \varphi}=\frac{m \omega^{2} R_{Z} \cos \varphi}{m g}=\frac{\omega^{2} R_{Z} \cos \varphi}{g}=0,0035 \cos \varphi$$где величину $\frac{\omega^{2} R_{Z}}{g}$ можно рассчитать, если учесть, что радиус Земли равен Rz=6400 км. Угловая скорость вращения Земли есть:
$$\omega=\frac{2 \pi}{T}=\frac{2 \pi}{86400}$$Получаем, что:
$$\sin \alpha=0,0035 \cos \varphi \sin \varphi=0,0018 \sin (2 \varphi)$$Ответ. $\sin \alpha \approx 0,0018 \sin (2 \varphi)$
Читать дальше: Формула ускорения.










