Векторное произведение радиус – вектора ($\bar{r}$), который проведен из точки О (рис.1) в точку к которой приложена сила $\bar{F}$ на сам вектор $\bar{F}$ называют моментом силы ($\bar{M}$) по отношению к точке O:
$$\bar{M}=\bar{r} \times \bar{F}(1)$$Содержание:
- Определение и формула момента силы
- Момент силы относительно оси
- Главный момент сил
- Основной закон динамики вращательного движения
- Единицы измерения момента силы
- Примеры решения задач
Определение и формула момента силы
Определение

На рис.1 точка О и вектор силы ( $\bar{F}$)и радиус – вектор $\bar{r}$ находятся в плоскости рисунка. В таком случае вектор момента силы ($\bar{M}$) перпендикулярен плоскости рисунка и имеет направление от нас. Вектор момента силы является аксиальным. Направление вектора момента силы выбирается таким образом, что вращение вокруг точки О в направлении силы и вектор $\bar{M}$ создают правовинтовую систему. Направление момента сил и углового ускорения совпадают.
Величина вектора $\bar{M}$ равна:
$$M=r F \sin \alpha=l F$$где $\alpha$ – угол между направлениями радиус – вектора и вектора силы, $l=r \sin \alpha$– плечо силы относительно точки О.
Момент силы относительно оси
Моментом силы по отношению к оси является физическая величина, равная проекции вектора момента силы относительно точки избранной оси на данную ось. При этом выбор точки значения не имеет.
Главный момент сил
Главным моментом совокупности сил относительно точки О называется вектор $\bar{M}$ (момент силы), который равен сумме моментов всех сил, действующих в системе по отношению к той же точке:
$$\bar{M}=\sum_{i=1}^{k} \bar{M}_{i}=\sum_{i=1}^{k} \bar{r}_{i} \times \bar{F}_{i}(3)$$При этом точку О называют центром приведения системы сил.
Если имеются два главных моменты ($\bar{M}$ и $\overline{M^{\prime}}$)для одной системы сил для разных двух центров приведение сил (О и О’), то они связаны выражением:
$$\bar{M}^{\prime}=\bar{M}-\bar{r}_{O^{\prime}} \times \bar{F}(4)$$где $\bar{r}_{O^{\prime}}$ - радиус-вектор, который проведен из точки О к точке О’, $\bar{F}$ – главный вектор системы сил.
В общем случае результат действия на твердое тело произвольной системы сил такое же, как действие на тело главного момента $\bar{M}$ системы сил и главного вектора системы сил, который приложен в центре приведения (точка О).
Основной закон динамики вращательного движения
$$\bar{M}=\frac{d \bar{L}}{d t}$$где $\bar{L}$ – момент импульса тела находящегося во вращении.
Для твердого тела этот закон можно представить как:
$$\bar{M}=I \bar{\varepsilon}(6)$$где I – момент инерции тела, $\bar{\varepsilon}$ – угловое ускорение.
Единицы измерения момента силы
Основной единицей измерения момента силы в системе СИ является: [M]=Н•м
В СГС: [M]=дин•см
Примеры решения задач
Пример
Задание. На рис.1 показано тело, которое имеет ось вращения OO'. Момент силы, приложенный к телу относительно заданной оси, будет равен нулю? Ось и вектор силы расположены в плоскости рисунка.

Решение. За основу решения задачи примем формулу, определяющую момент силы:
$$\bar{M}=\bar{r} \times \bar{F}(1.1)$$В векторном произведении (видно из рисунка) $\bar{r} \neq 0, \bar{F} \neq 0$ . Угол между вектором силы и радиус – вектором также будет отличен от нуля (или $180^{\circ}$), следовательно, векторное произведение (1.1) нулю не равно. Значит, момент силы отличен от нуля.
Ответ. $\bar{M} \neq 0$
Пример
Задание. Угловая скорость вращающегося твердого тела изменяется в соответствии с графиком, который представлен на рис.2. В какой из указанных на графике точек момент сил, приложенных к телу равен нулю?
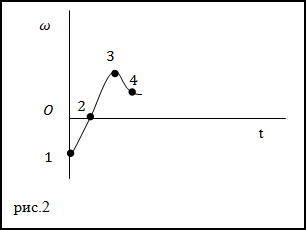
Решение. Момент сил, приложенных к вращающемуся твердому телу можно найти при помощи основного закона вращательного движения:
$$M=I \varepsilon(2.1)$$где $\varepsilon$ угловое ускорение вращения тела.его в свою очередь можно выразить через угловую скорость вращения тела как:
$$\varepsilon=\frac{d \omega}{d t}(2.2)$$Перепишем (2.1), используя (2.2), имеем:
$$M=I \frac{d \omega}{d t}(2.3)$$Так как $I \neq 0$ (момент инерции не равен нулю), то для выполнения условия M=0 должна быть равна нулю производная от угловой скорости по времени. Производная равна нулю в экстремуме. На рис. экстремумом является точка 3.
Ответ. M=0 в точке 3.
Читать дальше: Формула мощности.










