Электрическим током называют упорядоченное движение носителей зарядов. В металлах таковыми являются электроны, отрицательно заряженные частицы с зарядом, равным элементарному заряду. Направлением тока считают направление движения положительно заряженных частиц.
Содержание:
- Определение и формула силы тока
- Некоторые виды силы тока
- Плотность тока
- Сила тока в соединениях проводников
- Закон Ома
- Единицы измерения силы тока
- Примеры решения задач
Определение и формула силы тока
Определение
Силой тока (током) через некоторую поверхность S называют скалярную физическую величину, которую обозначают I, равную:
$$I=\frac{d q}{d t}$ (1)$где q – заряд, проходящий сквозь поверхность S, t – время прохождения заряда. Выражение (1) определяет величину силы тока в момент времени t (мгновенное значение величины силы тока).
Некоторые виды силы тока
Ток носит название постоянного, если его сила и направление с течением времени не изменяются, тогда:
$$I=\frac{q}{t}(2)$$Формула (2) показывает, что сила постоянного тока равна заряду, который проходит сквозь поверхность S в единицу времени.
Если ток является переменным, то выделяют мгновенную силу тока (1), амплитудную силу тока и эффективную силу тока. Эффективной величиной силы переменного тока (Ieff) называют такую силу постоянного тока, которая выполнит работу равную работе переменного тока в течение одного периода (T):
$$I_{e f f}=\sqrt{\frac{1}{T} \int_{0}^{T} I^{2} d t}(3)$$Если переменный ток можно представить как синусоидальный:
$$I=I_{m} \sin \omega t$$то Im – амплитуда силы тока ($\omega$ – частота силы переменного тока).
Плотность тока
Распределение электрического тока по сечению проводника характеризуют при помощи вектора плотности тока ($\bar{j}$). При этом:
$$j_{n}=j \cos \alpha=\frac{d I}{d S}(5)$$где $\alpha$ – угол между векторами $\bar{j}$ и $\bar{n}$ ( $\bar{n}$ – нормаль к элементу поверхности dS), jn – проекция вектора плотности тока на направление нормали ($\bar{n}$).
Сила тока в проводнике определяется при помощи формулы:
$$I=\int_{S} j d S(6)$$где интегрирование в выражении (6) проводится по всему поперечному сечению проводника S ($\alpha \equiv 0$)
Для постоянного тока имеем:
$I = jS (7)$Если рассматривать два проводника с сечениями S1 и S2 и постоянными токами, то выполняется соотношение:
$$\frac{j_{1}}{j_{2}}=\frac{S_{2}}{S_{1}}(8)$$Сила тока в соединениях проводников
При последовательном соединении проводников сила тока в каждом из них одинакова:
$$I=I_{1}=I_{2}=\cdots=I_{i}(9)$$При параллельном соединении проводников сила тока (I) вычисляется как сумма токов в каждом проводнике (Ii):
$$I=\sum_{i=1}^{n} I_{i}(10)$$Закон Ома
Сила тока входит в один из основных законов постоянного тока – закон Ома (для участка цепи):
$$I=\frac{\varphi_{1}-\varphi_{2}+\varepsilon}{R}(11)$$где $\varphi_{1}$ - $\varphi_{2}$ – разность потенциалов на концах, рассматриваемого участка, $\varepsilon$ - ЭДС источника, который входит в участок цепи, R – сопротивление участка цепи.
Единицы измерения силы тока
Основной единицей измерения силы тока в системе СИ является: [I]=A(ампер)=Кл/с
Примеры решения задач
Пример
Задание. Какой заряд (q) проходит через поперечное сечение проводника за промежуток времени от t1=2c до t2=6c, если сила тока изменяется в соответствии с уравнением: I=2+t, где сила тока в амперах, время в секундах?
Решение. За основу решения задачи примем определение мгновенной силы тока:
$$I=\frac{d q}{d t}$$В таком случае, заряд, который проходит через поперечное сечение проводника, равен:
$$q=\int_{t_{1}}^{t_{2}} I d t(1.2)$$Подставим в выражение (1.2) уравнение для силы тока из условий задачи, примем во внимания границы изменения участка времени:
$q=\int_{2}^{6}(2+t) d t=2 t+\left.\frac{t^{2}}{2}\right|_{2} ^{6}=(30-6)=24$ (Кл)
Ответ. q=24 Кл
Пример
Задание. Плоский конденсатор составлен из двух квадратных пластин со стороной A, находящихся на расстоянии dдруг от друга. Этот конденсатор подключен к источнику постоянного напряжения U. Конденсатор погружают в сосуд с керосином (пластины конденсатора вертикальны) со скоростью v=const. Какова сила тока, которая будет течь по подводящим проводам в описанном выше процессе. Считать, что диэлектрическая проницаемость керосина равна $\varepsilon$.
Решение. Основой для решения задачи станет формул для вычисления силы тока вида:
$$I=\frac{d q}{d t}(2.1)$$При погружении в керосин на глубину xописанной выше системы мы получаем два конденсатора, соединенных параллельно (над керосином и в керосине) рис. 2. Для такой системы конденсаторов напряжение на каждом из них одинаково, поэтому уравнение для изменения заряда при движении удобно искать в виде:
$dq = UdC (2.2)$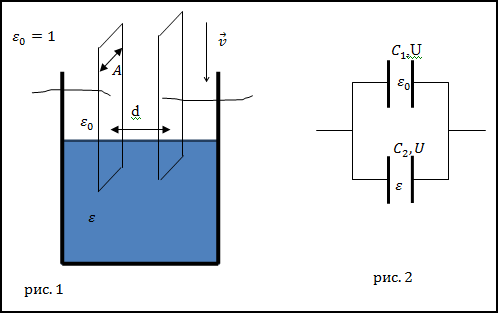
Емкость при параллельном соединении конденсаторов равна:
$C = C_1 + C_2 (2.3)$Формула для расчета емкостей C1 и C2 плоских конденсаторов имеет вид:
$$C_{1}=\frac{\varepsilon_{0}(A \cdot(A-v t))}{d}=\frac{\varepsilon_{0}}{d}\left(A^{2}-A v t\right) \rightarrow C_{2}=\frac{\varepsilon \varepsilon_{0}(A v t)}{d}(2.4)$$где $\varepsilon_{0}$ – электрическая постоянная, переменной величиной при погружении системы в керосин является площадь обкладок S:
$$S_{2}=A \cdot v \cdot t ; S_{1}=A \cdot(A-v t)$$Из выражений (2.4), (2.5) и условий задачи имеем:
$$d C=d C_{1}+d C_{2}=\frac{\varepsilon \varepsilon_{0} A v d t}{d}-\frac{\varepsilon_{0}}{d} A v d t(2.6)$$Тогда подставив dC в формулу для силы тока (2.1) получаем:
$$I=U\left(\frac{\varepsilon \varepsilon_{0} A v}{d}-\frac{\varepsilon_{0}}{d} A v\right)=\frac{\varepsilon_{0} U A v}{d}(\varepsilon-1)$$Ответ. $I=\frac{\varepsilon_{0} U A v}{d}(\varepsilon-1)$
Читать дальше: Формула силы.










