Задание. Вычислить производную функции $y(x)=\left(x^{2}-1\right)^{4}$
Решение. Искомая производная равна:
$$y^{\prime}(x)=\left(\left(x^{2}-1\right)^{4}\right)^{\prime}$$
Далее находим производную по формуле, но учитываем, что основание степени есть что-то более сложное, чем
$x$ (то есть ищем производную от сложной функции),
то умножаем еще все на производную от основания степени:
$$y^{\prime}(x)=4 \cdot\left(x^{2}-1\right)^{4-1} \cdot\left(x^{2}-1\right)^{\prime}$$
В первом множителе упрощаем степень, а также находим производную, учитывая тот факт, что
производная от суммы равна сумме производных:
$$y^{\prime}(x)=4\left(x^{2}-1\right)^{3} \cdot\left[\left(x^{2}\right)^{\prime}-(1)^{\prime}\right]$$
Находя производные от степенной функции и от константы, получаем:
$$y^{\prime}(x)=4\left(x^{2}-1\right)^{3} \cdot(2 x-0)$$
Упрощаем полученное выражение:
$$y^{\prime}(x)=8 x\left(x^{2}-1\right)^{3}$$
Ответ. $y^{\prime}(x)=8 x\left(x^{2}-1\right)^{3}$
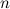 может быть как
может быть как










