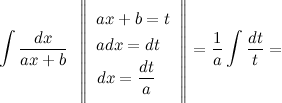Такой интеграл находится с помощью замены переменных:

$$=\frac{1}{a} \ln |t|+C=\frac{1}{a} \ln |a x+b|+C$$

Пример

Задание. Найти интеграл $\int \frac{d x}{3 x-4}$

Решение. Сделаем замену переменной: $3x-4=t$

$$\int \frac{d x}{3 x-4}\left\|\begin{array}{l} 3 x-4=t \\ 3 d x=d t \\ d x=\frac{d t}{3} \end{array}\right\|=\frac{1}{3} \int \frac{d t}{t}=$$ $$=\frac{1}{3} \ln |t|+C=\frac{1}{3} \ln |3 x-4|+C$$

Ответ. $\int \frac{d x}{3 x-4}=\frac{1}{3} \ln |3 x-4|+C$

Читать дальше: интегрирование правильных рациональных дробей.

Warning: file_put_contents(./students_count.txt): failed to open stream: Permission denied in /var/www/webmath-q2ws/data/www/webmath.ru/poleznoe/guide_content_banner.php on line 20
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 463 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!