Рациональная дробь $\frac{P_{m}(x)}{Q_{n}(x)}=\frac{a_{0}+a_{1} x+a_{2} x^{2}+\ldots+a_{m} x^{m}}{b_{0}+b_{1} x+b_{2} x^{2}+\ldots+b_{n} x^{n}}$ называется правильной, если степень многочлена числителя меньше степени многочлена знаменателя, т.е. $m < n$. Если же $m \geq n$, то дробь называется неправильной.
Определение
Пример
Рациональная дробь $\frac{x+1}{x^{2}-2}$ является правильной.
Выражения $\frac{x^{2}+1}{x^{2}-2}$ и $\frac{x^{3}-3 x+1}{x^{2}-2}$ - неправильные рациональные дроби.
Если дробь неправильная, то, разделив числитель на знаменатель по правилу деления многочленов, можно получить многочлен плюс правильную дробь.
Примеры интегрирования правильных рациональных дробей
Пример
Задание. Представить неправильную дробь $\frac{x^{2}+x-7}{x+1}$ в виде суммы многочлена и правильной дроби.
Решение. Поделим числитель на знаменатель дроби в столбик (деление проводится до тех пор, пока степень остатка не будет меньше степени делителя):
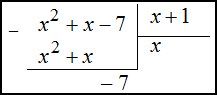
Таким образом,
$$\frac{x^{2}+x-7}{x+1}=x+\frac{-7}{x+1}=x-\frac{7}{x+1}$$Ответ. $\frac{x^{2}+x-7}{x+1}=x-\frac{7}{x+1}$
Пример
Задание. Найти интеграл $\int \frac{x^{2}-2 x+2}{x-1} d x$
Решение. Так как подынтегральная функция $\frac{x^{2}-2 x+2}{x-1}$ является неправильной рациональной дробью (так как степень числителя больше степени знаменателя), то выделим целую часть, для этого числитель поделим на знаменатель в столбик:
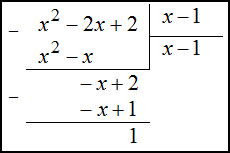
То есть,
$$\frac{x^{2}-2 x+2}{x-1}=x-1+\frac{1}{x-1}$$Тогда интеграл
$$\begin{array}{c} \int \frac{x^{2}-2 x+2}{x-1} d x=\int\left(x-1+\frac{1}{x-1}\right) d x= \\ =\int x d x-\int d x+\int \frac{d x}{x-1}=\frac{x^{2}}{2}-x+\ln |x-1|+C \end{array}$$Ответ. $\int \frac{x^{2}-2 x+2}{x-1} d x==\frac{x^{2}}{2}-x+\ln |x-1|+C$
Читать дальше: универсальная тригонометрическая подстановка.










