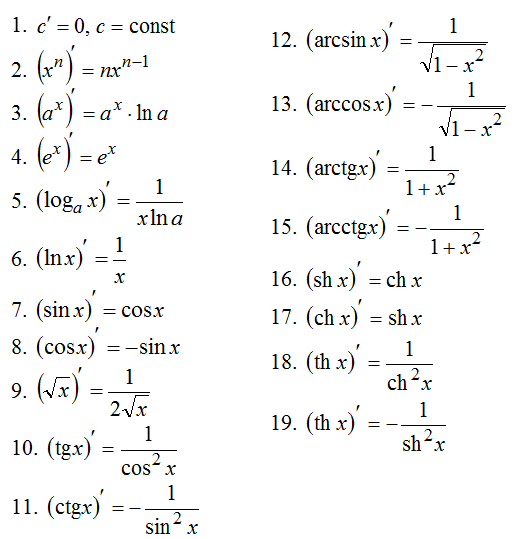Задание. Найти производную функции $y=x \cos x-\frac{e^{x}}{x}+4$
Решение. Используем правила дифференцирования и таблицу производных:
$$y^{\prime}=\left(x \cos x-\frac{e^{x}}{x}+4\right)^{\prime}=(x \cos x)^{\prime}-\left(\frac{e^{x}}{x}\right)^{\prime}+(4)^{\prime}=$$
$$=(x)^{\prime} \cdot \cos x+x \cdot(\cos x)^{\prime}-\frac{\left(e^{x}\right)^{\prime} \cdot x-e^{x} \cdot(x)^{\prime}}{x^{2}}+0=$$
$$\quad=1 \cdot \cos x+x \cdot(-\sin x)-\frac{e^{x} \cdot x-e^{x} \cdot 1}{x^{2}}=$$
$$=\cos x-x \sin x-\frac{x e^{x}-e^{x}}{x^{2}}=\cos x-x \sin x-\frac{(x-1) e^{x}}{x^{2}}$$
Ответ. $y^{\prime}=\cos x-x \sin x-\frac{(x-1) e^{x}}{x^{2}}$