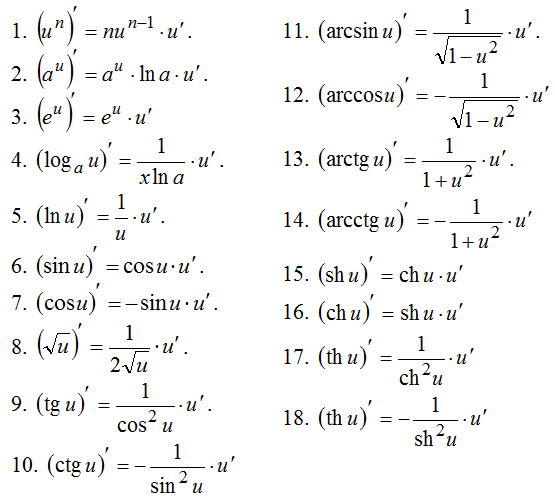Задание. Найти производную сложной функции $y=\sqrt{x^{2}-3 x+17}$
Решение. Используем правила дифференцирования и таблицу производных сложных функций:
$y^{\prime}=\left(\sqrt{x^{2}-3 x+17}\right)^{\prime}=\frac{1}{2 \sqrt{x^{2}-3 x+17}} \cdot\left(x^{2}-3 x+17\right)^{\prime}=$
$=\frac{1}{2 \sqrt{x^{2}-3 x+17}} \cdot\left[\left(x^{2}\right)^{\prime}-(3 x)^{\prime}+(17)^{\prime}\right]=$
$=\frac{1}{2 \sqrt{x^{2}-3 x+17}} \cdot\left[2 x^{2-1}-3 \cdot(x)^{\prime}+0\right]=$
$=\frac{1}{2 \sqrt{x^{2}-3 x+17}} \cdot(2 x-3 \cdot 1)=\frac{2 x-3}{2 \sqrt{x^{2}-3 x+17}}$
Ответ. $y^{\prime}=\frac{2 x-3}{2 \sqrt{x^{2}-3 x+17}}$