Содержание:

Касательная и нормаль к кривой

Определение

Касательная прямая - прямая, проходящая через точку кривой и совпадающая с ней в этой точке с точностью до первого порядка.

Определение

Прямая, проходящая через точку касания, перпендикулярно касательной, называется нормалью к кривой.

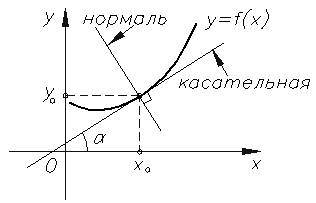
Если кривая определена уравнением $y=f(x)$, то уравнение касательной к ней в точке $M(x_0;y_0)$ имеет вид:

$$y-y_{0}=y^{\prime}\left(x_{0}\right)\left(x-x_{0}\right)$$

а уравнение нормали:

$$y-y_{0}=-\frac{1}{y^{\prime}\left(x_{0}\right)}\left(x-x_{0}\right)$$

Пример

Задание. Написать уравнение касательной и нормали к кривой $y=x^2-3x+4$ в точке с абсциссой $x_0=0$.

Решение. Находим значение функции в заданной точке:

$$y_0=y(x_0)=y(0)=4$$

Далее вычислим значение производной функции в точке $x_0=0$:

$$\begin{array}{l} y^{\prime}=\left(x^{2}-3 x+4\right)^{\prime}=\left(x^{2}\right)^{\prime}-(3 x)^{\prime}+(4)^{\prime}= \\ =2 x-3 \cdot(x)^{\prime}+0=2 x-3 \Rightarrow y^{\prime}(0)=-3 \end{array}$$

а тогда уравнение касательной запишется в виде:

$$y-4=-3(x-0)$$

или после упрощения:

$$3x+y-4=0$$

уравнение нормали:

$$y-4=-\frac{1}{-3}(x-0) \Rightarrow x-3 y+12=0$$

Ответ. Уравнение касательной: $3x+y-4=0$

Уравнение нормали: $x-3y+12=0$

Больше примеров решений Решение производных онлайн

Угол между кривыми

Определение

Углом между кривыми на плоскости в их общей точке $M(x_0;y_0)$ называется наименьший из двух возможных углов между касательными к этим кривым в данной точке. Если уравнения касательных, проведенных к кривым $y=f_1(x)$ и $y=f_2(x)$, соответственно $y=k_{1}x+b_{1}$ и $y=k_{2}x+b_2$, то тангенс угла между кривыми определяется соотношением:

$$\operatorname{tg} \phi=\frac{k_{2}-k_{1}}{1+k_{1} k_{2}}=\frac{f_{2}^{\prime}\left(x_{0}\right)-f_{1}^{\prime}\left(x_{0}\right)}{1+f_{1}^{\prime}\left(x_{0}\right) f_{2}^{\prime}\left(x_{0}\right)}$$

Warning: file_put_contents(./students_count.txt): failed to open stream: Permission denied in /var/www/webmath-q2ws/data/www/webmath.ru/poleznoe/guide_content_banner.php on line 20
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 469 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Найти тангенс угла между кривыми $y=x^2-1$ и $y=x^3-1$ в точке их пересечения, которая имеет большую абсциссу.

Решение. Вначале найдем точки пересечения графиков заданных функций, для этого совместно разрешим уравнение заданных кривых:

$$\begin{array}{c} \left\{\begin{array}{l} y_{1}=x^{2}-1 \\ y_{2}=x^{3}-1 \end{array} \Rightarrow x^{2}-1=x^{3}-1 \Rightarrow x^{3}-x^{2}=0 \Rightarrow\right. \\ \Rightarrow x_{1,2}=0, x_{3}=1 \end{array}$$

Таким образом, искомая точка $x=1$.

Далее находим производные заданных функций в найденной точке:

$$\begin{array}{c} y_{1}^{\prime}=\left(x^{2}-1\right)^{\prime}=\left(x^{2}\right)^{\prime}-(1)^{\prime}=2 x-0=2 x, y_{1}^{\prime}(1)=2 \\ y_{2}^{\prime}=\left(x^{3}-1\right)^{\prime}=\left(x^{3}\right)^{\prime}-(1)^{\prime}=3 x^{2}-0=3 x^{2}, y_{2}^{\prime}(1)=3 \end{array}$$

Итак, искомый тангенс:

$$\operatorname{tg} \phi=\frac{3-2}{1+2 \cdot 3}=\frac{1}{7}$$

Ответ. $\operatorname{tg} \phi=\frac{1}{7}$

Больше примеров решений Решение производных онлайн

Читать дальше: производные высших порядков.