Простыми дробями называются рациональные дроби вида $\frac{A}{(x-a)^{n}}$, $\frac{B x+C}{\left(x^{2}+p x+q\right)^{m}}$, где $n,m \geq 1$, $p^2-4q < 0$.
Содержание:
Основные понятия и определения
Определение
Теорема
(О разложении многочлена на элементарные множители)
Многочлен $n$-ой степени может быть разложен на произведение сомножителей следующим образом:
$P_{n}(x)=a_{0}\left(x-x_{1}\right)\left(x-x_{2}\right) \ldots\left(x-x_{n}\right)$Здесь $x_{i}, i=\overline{1 ; n}$ - корни многочлена $P_{n}x$, а $a_0$ - коэффициент при старшей степени $x^n$ указанного многочлена.
Квадратный трехчлен можно разложить на множители следующим образом:
$$a x^{2}+b x+c=a\left(x-x_{1}\right)\left(x-x_{2}\right)$$если $b^{2}-4 a c \geq 0$ . Здесь $x_1,x_2$ - корни многочлена $ax^2+bx+c$ .
Пример
Задание. Разложить на множители многочлен $f(x)=x^2+5x-6$
Решение. Найдем вначале корни многочлена, для этого решим уравнение $f(x)=0$ :
$$f(x)=0 \Rightarrow x^{2}+5 x-6=0$$Находим дискриминант:
$$D=b^{2}-4 a c=5^{2}-4 \cdot 1 \cdot(-6)=25+24=49$$ $$\sqrt{D}=\sqrt{49}=7$$Тогда
$$x_{1,2}=\frac{-b \pm \sqrt{D}}{2 a}=\frac{-5 \pm 7}{2 \cdot 1}=\frac{-5 \pm 7}{2}=\{1 ;-6\}$$Таким образом,
$$f(x)=x^{2}+5 x-6=1 \cdot(x-1)(x-(-6))=(x-1)(x+6)$$Можете проверить решение на нашем онлайн калькуляторе - решение квадратных уравнений.
Ответ. $f(x)=(x-1)(x+6)$
Многочлен третьей степени:
$$a x^{3}+b x^{2}+c x+d=a\left(x-x_{1}\right)\left(x-x_{2}\right)\left(x-x_{3}\right)$$или 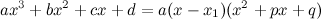 , если
$a x^{3}+b x^{2}+c x+d=a\left(x-x_{1}\right)\left(x^{2}+p x+q\right),$ ecли $p^{2}-4 q< 0$
, если
$a x^{3}+b x^{2}+c x+d=a\left(x-x_{1}\right)\left(x^{2}+p x+q\right),$ ecли $p^{2}-4 q< 0$
Пример
Задание. Разложить на множители кубический многочлен $f(x)=x^3-x^2-4x-6$
Решение. Найдем корни данного многочлена. Известно, что если многочлен имеет корни, то они являются делителем свободного коэффициента, то есть в данном случае 6, а это ±1,±2,±3,±6. Подставляем указанные значения в заданный многочлен:
$$\begin{array}{c} f(1)=1^{3}-1^{2}-4 \cdot 1-6=-10 \neq 0 \\ f(-1)=(-1)^{3}-(-1)^{2}-4 \cdot(-1)-6=-4 \neq 0 \\ f(2)=2^{3}-2^{2}-4 \cdot 2-6=-10 \neq 0 \\ f(-2)=(-2)^{3}-(-2)^{2}-4 \cdot(-2)-6=-10 \neq 0 \\ f(3)=3^{3}-3^{2}-4 \cdot 3-6=0 \end{array}$$Итак, один корень найден, это $x_1=3$ .
Для нахождения остальных двух корней поделим заданный многочлен $f(x)$ на двучлен $x-3$ в столбик (уголком):
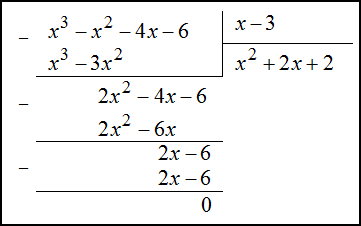
Тогда
$$f(x)=x^{3}-x^{2}-4 x-6=(x-3)\left(x^{2}+2 x+2\right)$$Находим теперь корни квадратного трехчлена $x^2+2x+2$ . Для этого приравниваем его к нулю и находим дискриминант:
$$x^{2}+2 x+2=0 \Rightarrow D=2^{2}-4 \cdot 1 \cdot 2=4-8=-4<0$$ \lt p>Таким образом, трехчлен $x^2+2x+2$ действительных корней не имеет.Итак, искомое разложение
$$f(x)=(x-3)\left(x^{2}+2 x+2\right)$$Ответ. $f(x)=(x-3)\left(x^{2}+2 x+2\right)$
Разложении правильной рациональной дроби
Теорема
(О разложении правильной рациональной дроби на сумму простых дробей)
Каждая рациональная дробь $\frac{P_{m}(x)}{Q_{n}(x)}$, знаменатель которой имеет вид $Q_{n}(x)=\left(x-x_{1}\right)^{n}\left(x-x_{2}\right)^{m} \ldots\left(x^{2}+p_{1} x+q_{1}\right)^{k} \ldots$ , может быть разложена и притом единственным образом на сумму простых дробей по правилу
$$\begin{aligned} \frac{P_{m}(x)}{Q_{n}(x)}=& \frac{A_{1}}{x-x_{1}}+\ldots+\frac{A_{n}}{\left(x-x_{1}\right)^{n}}+\frac{B_{1}}{x-x_{2}}+\ldots+\frac{B_{m}}{\left(x-x_{2}\right)^{m}}+\\ &+\frac{C_{1} x+D_{1}}{x^{2}+p_{1} x+q_{1}}+\ldots+\frac{F_{k} x+G_{k}}{\left(x^{2}+p_{1} x+q_{1}\right)^{k}}+\ldots \end{aligned}$$где $A_{1}, \ldots, A_{n} ; B_{1}, \ldots, B_{m} ; C_{1}, \ldots, C_{k}: D_{1}, \ldots, D_{k}$ - действительные постоянные числа, часть которых в разложении может обратиться в нуль.
В частности, если в знаменателе правильной рациональной дроби стоит квадратный трехчлен, то
$$\frac{P_{1}(x)}{\left(x-x_{1}\right)\left(x-x_{2}\right)}=\frac{A}{x-x_{1}}+\frac{B}{x-x_{2}}$$Пример
Задание. Представить в виде суммы простейших дробей дробь $\frac{x+1}{x^{2}+3 x-4}$ . Коэффициенты разложения находить ненужно.
Решение. Знаменатель рассматриваемой дроби можно разложить на множители следующим образом:
$$x^{2}+3 x-4=(x-1)(x+4)$$то есть
$$\frac{x+1}{x^{2}+3 x-4}=\frac{x+1}{(x-1)(x+4)}=\frac{A}{x-1}+\frac{B}{x+4}$$Ответ. $\frac{x+1}{x^{2}+3 x-4}=\frac{A}{x-1}+\frac{B}{x+4}$
Если многочлен третей степени, то в зависимости от числа и кратности действительных корней разложение будет иметь вид:
$$\frac{P_{2}(x)}{\left(x-x_{1}\right)\left(x-x_{2}\right)\left(x-x_{3}\right)}=\frac{A}{x-x_{1}}+\frac{B}{x-x_{2}}+\frac{C}{x-x_{3}}$$или
$$\frac{P_{2}(x)}{\left(x-x_{1}\right)\left(x-x_{2}\right)^{2}}=\frac{A}{x-x_{1}}+\frac{B}{x-x_{2}}+\frac{C}{\left(x-x_{2}\right)^{2}}$$или
$$\frac{P_{2}(x)}{\left(x-x_{1}\right)\left(x^{2}+p x+q\right)}=\frac{A}{x-x_{1}}+\frac{B x+C}{x^{2}+p x+q}$$Читать дальше: метод неопределенных коэффициентов.










