1.   $\left(x^{p}\right)^{(n)}=p(p-1)(p-2) \ldots(p-n+1) x^{p-n}$

Пример

Задание. Найти $(x^5)^{(4)}$

Решение. $p=5,n=4$, согласно формуле №1 получаем:

$$\left(x^{5}\right)^{(4)}=5 \cdot 4 \cdot 3 \cdot(5-4+1) x^{5-4}=120 x$$

Ответ. $(x^5)^{(4)}=120x$

2.   $\left(a^{k x+b}\right)^{(n)}=k^{n} a^{k x+b} \ln ^{n} a$


Warning: file_put_contents(./students_count.txt): failed to open stream: Permission denied in /var/www/webmath-q2ws/data/www/webmath.ru/poleznoe/guide_content_banner.php on line 20
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 456 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Найти производную пятого порядка функции $y=3^{5x-3}$

Решение. Согласно формуле №2 получаем:

$$y^{(5)}=\left(3^{5 x-3}\right)^{(5)}=5^{5} \cdot 3^{5 x-3} \cdot \ln ^{5} 3=3125 \ln ^{5} 3 \cdot 3^{5 x-3}$$

Ответ. $y^{(5)}=3125 \ln ^{5} 3 \cdot 3^{5 x-3}$

3.   $\left(e^{k x+b}\right)^{(n)}=k^{n} e^{k x+b}$

Пример

Задание. Найти $y^{6}(x)$, если $y(x)=e^{4x}$

Решение. Согласно формуле №3 получаем:

$$y^{(6)}(x)=\left(e^{4 x}\right)^{(6)}=4^{6} \cdot e^{4 x}=4096 e^{4 x}$$

Ответ. $y^{(6)}(x)=4096 e^{4 x}$

4.   $(\sin a x)^{(n)}=a^{n} \sin \left(a x+\frac{\pi n}{2}\right)$


Пример

Задание. Найти производную пятого порядка от функции $y(x)=\sin 5 x$

Решение. Согласно формуле №4 получаем:

$$y^{(5)}(x)=(\sin 5 x)^{(5)}=5^{5} \cdot \sin \left(5 x+\frac{5 \pi}{2}\right)=3125 \cos 5 x$$

Ответ. $y^{(5)}(x)=(\sin 5 x)^{(5)}=5^{5} \cdot \sin \left(5 x+\frac{5 \pi}{2}\right)=3125 \cos 5 x$

5.   $(\cos a x)^{(n)}=a^{n} \cos \left(a x+\frac{\pi n}{2}\right)$


Пример

Задание. Найти $(\cos 3 x)^{(7)}$

Решение. Согласно формуле №5 получаем:

$$(\cos 3 x)^{(7)}=3^{7} \cdot \cos \left(3 x+\frac{7 \pi}{2}\right)=2187 \sin 3 x$$

Ответ. $(\cos 3 x)^{(7)}=2187 \sin 3 x$

6.   $\left((a x+b)^{p}\right)^{(n)}=a^{n} p(p-1)(p-2) \ldots(p-n+1)(a x+b)^{p-n}$

Пример

Задание. Найти четвертую производную функции $y(x)=(4 x-7)^{8}$

Решение. Согласно формуле №6 получаем:

$$\begin{array}{c} y^{(4)}(x)=\left((4 x-7)^{8}\right)^{(4)}= \\ =4^{4} \cdot 8 \cdot 7 \cdot 6 \cdot 5 \cdot(4 x-7)^{8-4}=430080(4 x-7)^{4} \end{array}$$

Ответ. $y^{(4)}(x)=430080(4 x-7)^{4}$

7.   $\left(\log _{a}|x|\right)^{(n)}=\frac{(-1)^{n-1}(n-1) !}{x^{n} \ln a}$


Пример

Задание. Найти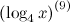

Решение. Согласно формуле №7 получаем:

$$\left(\log _{4} x\right)^{(9)}=\frac{(-1)^{9-1} \cdot(9-1) !}{x^{9} \cdot \ln 4}=\frac{(-1)^{8} \cdot 8 !}{x^{9} \cdot \ln 4}=\frac{8 !}{x^{9} \cdot \ln 4}$$

Ответ. $\left(\log _{4} x\right)^{(9)}=\frac{8 !}{x^{9} \cdot \ln 4}$

8.   $(\ln |x|)^{(n)}=\frac{(-1)^{n-1}(n-1) !}{x^{n}}$

9.   $(\alpha u(x)+\beta v(x))^{(n)}=\alpha u^{(n)}(x)+\beta v^{(n)}(x)$

10.   Формула Лейбница:

$$(u v)^{(n)}=u^{(n)} v+C_{n}^{1} u^{(n-1)} v^{\prime}+C_{n}^{2} u^{(n-2)} v^{\prime \prime}+\ldots+C_{n}^{n-1} u^{\prime} v^{(n-1)}+u v^{(n)}$$

Здесь $C_{n}^{k}=\frac{n !}{k !(n-k) !}$ - число комбинаций, $n !=1 \cdot 2 \cdot \ldots \cdot n$ - факториал натурального числа $n$.


Читать дальше: дифференциалы высших порядков.