Приращением аргумента называется разность между двумя значениями аргумента: "новым" и "старым".
Обычно обозначается как $\Delta x=x_{1}-x_{0}$ .
Содержание:
Пусть задана некоторая функция $y=f(x)$. Возьмем какое-нибудь значение $x_{0}$ из области определения этой функции: $x_{0} \in D[f]$ . Соответствующее значение функции в этой точке будет равно $y_{0}=f\left(x_{0}\right)$ .
Приращение аргумента и функции
Определение
Пример
Задание. Найти приращение аргумента $x$, если он переходит от значения 3 к значению 3,2.
Решение. Искомое приращение: $\Delta x=3,2-3=0,2$ .
Ответ. $\Delta x=0,2$
Зададим аргументу $x_{0}$ приращение $\Delta x$. А тогда значение функции в новой точке $f\left(x_{0}+\Delta x\right)$.
Определение
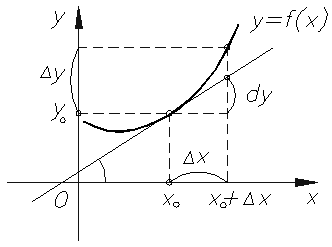
Приращением функции $y=f(x)$ в точке $x_{0}$, соответствующее приращению аргумента $\Delta x=x-x_{0}$, называется величина:
$\Delta y=f\left(x_{0}+\Delta x\right)-f\left(x_{0}\right)$
Warning: file_put_contents(./students_count.txt): failed to open stream: Permission denied in /var/www/webmath-q2ws/data/www/webmath.ru/poleznoe/guide_content_banner.php on line 20
Пример
Задание. Найти приращение функции $y=2 x^{2}$ при $x_{0}=3$ и $\Delta x=0,1$
Решение. Подставляя в формулу, получаем, что приращение функции:
$\Delta y=y(3+0,1)-y(3)=2 \cdot(3+0,1)^{2}-2 \cdot 3^{2}=1,22$
Ответ. $\Delta y=1,22$
Определение производной
Определение
Производной $y^{\prime}(x)$ от функции $y=f(x)$ в точке $x_{0}$ называется предел отношения приращения функции $\Delta y$ к приращению аргумента $\Delta x$ : $\frac{\Delta y}{\Delta x}$ при $\Delta x \rightarrow 0$, если он существует, то есть:
$y^{\prime}\left(x_{0}\right)=f^{\prime}\left(x_{0}\right)=\lim _{\Delta x \rightarrow 0} \frac{\Delta y}{\Delta x}=\lim _{\Delta x \rightarrow 0} \frac{f\left(x_{0}+\Delta x\right)-f\left(x_{0}\right)}{\Delta x}$
или
$y^{\prime}\left(x_{0}\right)=\lim _{x \rightarrow x_{0}} \frac{f(x)-f\left(x_{0}\right)}{x-x_{0}}$
Пример
Задание. Найти производную функции $y=x^{2}+3 x$ в точке $x_{0}=0$.
Решение. Найдем приращение заданной функции в точке $x_{0}$ :
$\Delta y=y(0+\Delta x)-y(0)=y(\Delta x)-y(0)=$
$=(\Delta x)^{2}+3 \Delta x-0=\Delta x(\Delta x+3)$
Тогда
$y^{\prime}(0)=\lim _{\Delta x \rightarrow 0} \frac{\Delta x(\Delta x+3)}{\Delta x}=\lim _{\Delta x \rightarrow 0}(\Delta x+3)=0+3=3$
Ответ. $y^{\prime}(0)=3$
Дифференцирование функции
Определение
Операция нахождения производной функции называется дифференцированием этой функции.
Функция $y=f(x)$ имеет производную на интервале $(a ; b)$ или называется дифференцируемой в этом интервале, если производная $f^{\prime}(x)$ существует в каждой точке этого интервала.
Функция $y=f(x)$ имеет в точке $x$ бесконечную производную, если в этой точке $f^{\prime}(x)=\lim _{\Delta x \rightarrow 0} \frac{\Delta y}{\Delta x}=\infty$ .
Теорема
(О непрерывности функции в точке)
Если функция $y=f(x)$ имеет конечную производную в точке $x_{0}$ , то она непрерывна в этой точке.
Замечание. Обратное заключение не всегда верно: если функция $y=f(x)$ непрерывна в некоторой точке $x_{0}$ , то она может и не иметь производной в этой точке.
Определение
Функция $y=f(x)$ называется дифференцируемой в точке $x$, если приращение функции, соответствующее приращению аргумента, можно представить в виде:
$\Delta y=A \cdot \Delta x+\alpha(\Delta x) \cdot \Delta x$
где $A$ - число, не зависящее от $\Delta x$, $\alpha(\Delta x)$ - б.м. функция при $\Delta x \rightarrow 0$.
Теорема
(О необходимом и достаточном условии дифференцируемости)
Для того чтобы функция $y=f(x)$ была дифференцируемой в точке $x$, необходимо и достаточно, чтобы $y=f(x)$ имела в этой точке конечную производную.
Теорема устанавливает, что для функции $y=f(x)$ дифференцируемость в данной точке $x$ и существование конечной производной в этой точке - понятия равносильные.
Читать дальше: односторонние производные.
Статьи по теме
Поможем выполнить
любую работу
