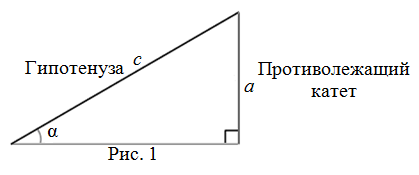
Синусом острого угла прямоугольного треугольника называется отношение противолежащего этому углу катета к гипотенузе (рис. 1):
Содержание:
Синус угла в треугольнике
Определение
Пример
Задание. Пусть задан прямоугольный треугольник, у которого гипотенуза равна 5 см, а один из катетов 3 см. Найти синус противолежащего этому катету угла.
Решение. Согласно определению имеем, что искомое значение равно отношению противолежащего катета к гипотенузе, то есть
$$\sin \alpha=\frac{3}{5}$$Ответ. $\sin \alpha=\frac{3}{5}$
Синус произвольного угла
Определение
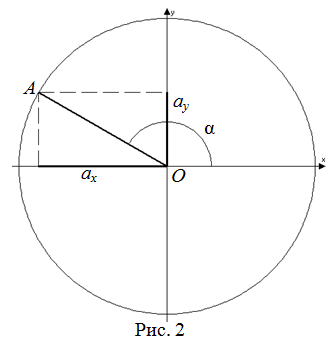
Синусом произвольного угла $\alpha$, образованного осью $Ox$ и произвольным радиус вектором $\overline{O A}=\left(a_{x} ; a_{y}\right)$ (рисунок 2), называется отношение проекции этого вектора на ось $Oy$ к его длине $a=|\overline{O A}|$:
Пример
Задание. Найти синус угла, образованного вектором $\bar{a}=(-1 ; 2)$ с осью абсцисс.
Решение. Согласно определению синуса угла получаем:
$\sin \alpha=\frac{2}{\sqrt{(-1)^{2}+2^{2}}}=\frac{2}{\sqrt{5}}=\frac{2 \sqrt{5}}{5}$Ответ. $\sin \alpha=\frac{2 \sqrt{5}}{5}$
Читать дальше: что такое косинус угла.










