Теорема

Пусть заданы две последовательности $\{x_n\}$ и $\{y_n\}$ . Если $\lim _{n \rightarrow \infty} x_{n}=a, \lim _{n \rightarrow \infty} y_{n}=b$ и, начиная с некоторого номера, $x_n \leq y_n$ , то выполняется неравенство: $a \leq b$

Теорема

(Принцип двустороннего ограничения, теорема о двух милиционерах, теорема сжатия, правило сэндвича, теорема о трех струнах).

Если $\lim _{n \rightarrow \infty} x_{n}=\lim _{n \rightarrow \infty} y_{n}=a$ и существует номер $n_{0} \in N$ , что для любого $n \geq n_{0}$ выполняется неравенство $x_{n} \leq z_{n} \leq y_{n}$ , то последовательность $\{z_n\}$ сходится, причем $\lim _{n \rightarrow \infty} z_{n}=a$

Пример

Задание. Найти предел последовательности $\left\{z_{n}\right\}=\left\{\frac{n}{n^{2}+1}\right\}$

Решение. С одной стороны $z_{n}=\frac{n}{n^{2}+1}>0=x_{n}, \forall n \in N$ . С другой стороны:

$$z_{n}=\frac{n}{n^{2}+1} \lt \frac{n}{n^{2}}=\frac{1}{n}=y_{n}$$

То есть, имеем: $0<\frac{n}{n^{2}+1}<\frac{1}{n}$ и из того, что $\lim _{n \rightarrow \infty} x_{n}=\lim _{n \rightarrow \infty} 0=0$ , $\lim _{n \rightarrow \infty} y_{n}=\lim _{n \rightarrow \infty} \frac{1}{n}=0$, то по теореме про двустороннее ограничение и $\lim _{n \rightarrow \infty} z_{n}=\lim _{n \rightarrow \infty} \frac{n}{n^{2}+1}=0$ :

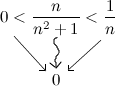
Читать дальше: предел монотонной последовательности, теорема Вейерштрасса.

Warning: file_put_contents(./students_count.txt): failed to open stream: Permission denied in /var/www/webmath-q2ws/data/www/webmath.ru/poleznoe/guide_content_banner.php on line 20
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 473 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!