Представление 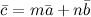 называется разложением вектора
называется разложением вектора
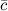 по компонентам
по компонентам 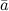 и
и
 . Если векторы
. Если векторы 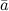 и
и
 не коллинеарны, то приведенное
представление единственно.
не коллинеарны, то приведенное
представление единственно.
Для двух коллинеарных векторов 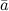 и
и
 всегда имеет место соотношение:
всегда имеет место соотношение:
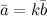 , где
, где
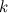 - некоторое ненулевое число.
- некоторое ненулевое число.
Если ввести в рассмотрение единичный вектор
(или орт) 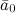 ,
длина которого равна единице:
,
длина которого равна единице: 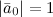 и который коллинеарен
вектору
и который коллинеарен
вектору 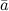 , то последний можно представить в виде:
, то последний можно представить в виде:
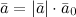
Произвольный вектор 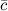 можно представить в виде:
можно представить в виде:
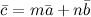 , где
, где
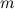 ,
, 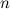 - произвольные числа, а тройка векторов
- произвольные числа, а тройка векторов
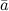 ,
,  и
и 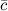 компланарна (рис. 1).
компланарна (рис. 1).
Определение
Для трех попарно неколлинеарных векторов 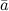 ,
,  и
и 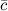 и произвольного вектора
и произвольного вектора
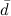 существует единственное разложение:
существует единственное разложение:
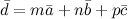
Читать дальше: проекция вектора на ось.










