Задание. Вычислить  , если
, если

Решение. Перепишем данное выражение, используя свойство логарифма степени и логарифма произведения:

Ответ. 
Интеграл функции является основным понятием интегрального исчисления. Интеграл широко используется при решении целого ряда задач по математике, физике и в других науках. Именно поэтому мы собрали на сайте более 100 примеров решения интегралов и постоянно добавляем новые! Список тем находится в правом меню.
Перед изучением примеров вычисления интегралов советуем вам прочитать теоретический материал по теме: определения, свойства и таблицу интегралов, методы их вычисления и другой материал по интегралам.
Логарифмы (Логарифмирование) активно используются в решении задач, так как значительно упрощают обычные алгебраические операции. Использование логарифмов позволяет заменить умножение на значительно более простое сложение, деление — на вычитание, а возведение в степень и извлечение корня заменяются соответственно на умножение и деление на показатель степени числа.
Перед изучением примеров решения задач советуем изучить теоретический материал по логарифмам, прочитать определения и все свойства логарифмов. Список тем находится в правом меню.
Основные ссылки - теоретический материал и примеры решений (10 шт).
Задание. Вычислить  , если
, если

Решение. Перепишем данное выражение, используя свойство логарифма степени и логарифма произведения:

Ответ. 
Основные ссылки - теоретический материал и примеры решений (10 шт).
Задание. Вычислить 
Решение. Преобразуем данное выражение, используя свойство суммы логарифмов и определение натурального логарифма:

Ответ. 
Основные ссылки - теоретический материал и примеры решений (10 шт).
Задание. Вычислить 
Решение. Преобразуем данное выражение, используя свойство логарифма степени, а также тот факт, что
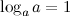 :
:
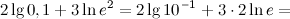
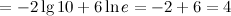
Ответ. 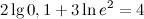
Основные ссылки - теоретический материал и примеры решений (10 шт).
Задание. Решить уравнение 
Решение. ОДЗ: 
Замена:  , получаем уравнение
, получаем уравнение
 . По определению логарифма:
. По определению логарифма:

Делая обратную замену, получаем:

Оба значения принадлежат ОДЗ.
Ответ. 
Основные ссылки - теоретический материал и примеры решений (10 шт).
Задание. Решить неравенство 
Решение. ОДЗ: 
Перейдем в неравенства от логарифмов к выражениям, стоящим под знаком логарифма, при этом, так как основание логарифма меньше единицы ( 0,5 < 1 ), знак неравенства поменяем на противоположный:
 или
или 
В пересечении с ОДЗ получаем, что 
Ответ. 
Программа не может допустить ошибки, у нее не может быть опечатки и ее почерк Вы всегда поймете. С нами решение задач по математике - это просто. Используйте наш сервис и решение задач по математике, физике, геометрии и теории вероятности не составит для Вас больше труда.
Для того, чтобы получить решение Вам надо только ввести данные и наши программы, самостоятельно, без участия людей, всего за пару секунд выдадут Вам точный, исчерпывающий ответ. Большинство программ вместе с ответом выдают подробное решение, в результате Вам надо только переписать решение в тетрадь и затем получить свою хорошую оценку. К программа прилагаются примеры решения задач, так что еще не введя данные, Вы будете знать, как будет выглядеть ответ. Для тренировки и усвоения материала используйте раздел примеры решения задач.
Все онлайн калькуляторы на сайте абсолютно бесплатны. Пользуйтесь на здоровье!