Задание. Найти производную функции 
Решение. Так как производная суммы равна сумме производных, то

Воспользуемся формулами для производных показательной и обратной тригонометрической функций:

Ответ. 
Интеграл функции является основным понятием интегрального исчисления. Интеграл широко используется при решении целого ряда задач по математике, физике и в других науках. Именно поэтому мы собрали на сайте более 100 примеров решения интегралов и постоянно добавляем новые! Список тем находится в правом меню.
Перед изучением примеров вычисления интегралов советуем вам прочитать теоретический материал по теме: определения, свойства и таблицу интегралов, методы их вычисления и другой материал по интегралам.
Производная функции является основным понятием дифференциального исчисления. Она характеризует скорость изменения функции в указанной точке. Производная широко используется при решении целого ряда задач по математике, физике и другим наукам, в особенности при изучении скорости различного рода процессов. Именно поэтому мы собрали на сайте более 200 примеров решения производных и постоянно добавляем новые! Список тем находится в правом меню.
Перед изучением примеров вычисления производных советуем изучить теоретический материал по теме: прочитать определения, правила дифференцирования, таблицу производных и другой материал по производным.
Основные ссылки - таблица производных, правила дифференцирования и примеры решений (10 шт).
Задание. Найти производную функции 
Решение. Так как производная суммы равна сумме производных, то

Воспользуемся формулами для производных показательной и обратной тригонометрической функций:

Ответ. 
Основные ссылки - теоретический материал и примеры решений (10 шт).
Задание.Найти производную функции 
Решение. По правилу дифференцирования сложной функции:

В свою очередь производная  также берется по правилу дифференцирования сложной функции:
также берется по правилу дифференцирования сложной функции:



Ответ. 
Основные ссылки - теоретический материал и примеры решений (10 шт).
Задание. Вычислить приближенно  ,
заменяя приращение функции ее дифференциалом.
,
заменяя приращение функции ее дифференциалом.
Решение. Рассмотрим функцию  .
Необходимо вычислить ее значение в точке
.
Необходимо вычислить ее значение в точке  .
Представим данное значение в виде следующей суммы:
.
Представим данное значение в виде следующей суммы:

Величины  и
и  выбираются так, чтобы в точке
выбираются так, чтобы в точке  можно было бы
достаточно легко вычислить значение функции и ее производной, а
можно было бы
достаточно легко вычислить значение функции и ее производной, а  было бы достаточно малой величиной. С учетом этого, делаем вывод, что
было бы достаточно малой величиной. С учетом этого, делаем вывод, что
 , то есть
, то есть
 ,
,
 .
.
Вычислим значение функции  в точке
в точке
 :
:

Далее продифференцируем рассматриваемую функцию и найдем значение
 :
:

Тогда

Итак,


Ответ. 
Основные ссылки - теоретический материал и примеры решений (10 шт).
Задание. Найти тангенс угла наклона касательной к графику функции
 в точке
в точке
 .
.
Решение. Из геометрического смысла производной получаем, что производная функции
 , вычисленная при заданном значении
, вычисленная при заданном значении
 , равна тангенсу угла, образованного
положительным направлением оси
, равна тангенсу угла, образованного
положительным направлением оси  и
положительным направлением касательной, проведенной к графику этой функции в точке с абсциссой
и
положительным направлением касательной, проведенной к графику этой функции в точке с абсциссой
 , то есть
, то есть

Найдем производную от заданной функции:

в точке  имеем:
имеем:

Тогда окончательно получим, что

Ответ. 
Основные ссылки - теоретический материал и примеры решений (10 шт).
Задание. Точка движется по закону  .
Чему равна скорость в момент времени
.
Чему равна скорость в момент времени  ?
?
Решение. Найдем скорость точки как первую производную от перемещения:


В момент времени  скорость равна
скорость равна

Ответ. 
Основные ссылки - теоретический материал и примеры решений (10 шт).
Задание. Записать уравнение касательной к графику функции
 в точке
в точке

Решение. Найдем значение функции в заданной точке:

Найдем производную заданной функции по правилу дифференцирования произведения:



Вычислим её значение в заданной точке

Используя формулу

запишем уравнение касательной:



Ответ. Уравнение касательной: 
Основные ссылки - теоретический материал и примеры решений (10 шт).
Задание. Найти производную второго порядка от функции

Решение. Находим первую производную как производную сложной функции:

Вторую производную находим как от произведения, предварительно вынеся по правилам дифференцирования коэффициент 3 за
знак производной. Также будем учитывать, что первый множитель -
 - есть сложной функцией:
- есть сложной функцией:




Ответ. 
Основные ссылки - теоретический материал и примеры решений (10 шт).
Задание. Уравнение движения материальной точки вдоль оси имеет вид
 (м). Найти ускорение
(м). Найти ускорение
 точки в момент времени
точки в момент времени
 c.
c.
Решение. Ускорение заданной точки найдем, взяв вторую производную от перемещения по времени:

Первая производная

 (м/с)
(м/с)
вторая производная
 (м/с2)
(м/с2)
В момент времени  c
c
 (м/с2)
(м/с2)
Ответ.  (м/с2)
(м/с2)
Основные ссылки - теоретический материал и примеры решений (10 шт).
Задание. Найти дифференциал третьего порядка функции 
Решение. По формуле

Найдем третью производную заданной функции:





Тогда

Ответ. 
Основные ссылки - теоретический материал и примеры решений (10 шт).
Задание. Найти производную неявно заданной функции

Решение. Продифференцируем обе части данного выражения по
 , учитывая, что
, учитывая, что
 функция от
функция от
 и производная от неё берется как от сложной функции.
и производная от неё берется как от сложной функции.


Выразим из этого равенства 




Ответ. 
Основные ссылки - теоретический материал и примеры решений (10 шт).
Задание. Найти производную 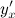 от функции заданной параметрически
от функции заданной параметрически

Решение. Найдем производные 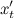 и
и
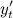


Подставляя найденные значения 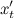 и
и
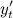 в формулу
в формулу
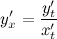
получим

Ответ. 
Основные ссылки - теоретический материал и примеры решений (10 шт).
Задание. Найти производную функции 
Решение. Применим логарифмическое дифференцирование:


Тогда, продифференцировав левую и правую часть, будем иметь:




Отсюда получаем, что

Ответ. 
Основные ссылки - теоретический материал и примеры решений (10 шт).
Задание. Разложить в ряд Тейлора функцию
 в точке
в точке
 .
.
Решение. Найдем производные:



Итак,  ,
,
 ,
,
 . Значение функции в точке
. Значение функции в точке

Таким образом,


Ответ. 
Программа не может допустить ошибки, у нее не может быть опечатки и ее почерк Вы всегда поймете. С нами решение задач по математике - это просто. Используйте наш сервис и решение задач по математике, физике, геометрии и теории вероятности не составит для Вас больше труда.
Для того, чтобы получить решение Вам надо только ввести данные и наши программы, самостоятельно, без участия людей, всего за пару секунд выдадут Вам точный, исчерпывающий ответ. Большинство программ вместе с ответом выдают подробное решение, в результате Вам надо только переписать решение в тетрадь и затем получить свою хорошую оценку. К программа прилагаются примеры решения задач, так что еще не введя данные, Вы будете знать, как будет выглядеть ответ. Для тренировки и усвоения материала используйте раздел примеры решения задач.
Все онлайн калькуляторы на сайте абсолютно бесплатны. Пользуйтесь на здоровье!