Свойства пределов функции

Содержание:

• Предел функции
• Свойства пределов функции

Предел функции

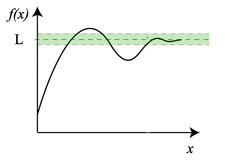
Предел функции — одно из основных понятий математического анализа. Функция f(x) имеет предел L в точке x₀, если для всех значений x, достаточно близких к x₀, значение f(x) близко к L.

Предел функции на бесконечности описывает поведение значения данной функции, когда её аргумент становится бесконечно большим (по абсолютной величине).

Предел функции обозначается как

$$f(x) \rightarrow L \quad$ при $\quad x \rightarrow a$$

или через символ предела функции:

$$\lim _{x \rightarrow 0} f(x)=L$$

Если при прочтении данного материала у Вас возникнут вопросы, Вы всегда можете задать их на нашем форуме, также на форуме Вам помогут решить задачи по математике, геометрии, химии, теории вероятности и многим другим предметам.

Свойства пределов функции

1) Предел постоянной величины

Предел постоянной величины равен самой постоянной величине:

$$\lim _{x \rightarrow a} C=C$$

2) Предел суммы

Предел суммы двух функций равен сумме пределов этих функций:

$$\lim _{x \rightarrow a}[f(x)+g(x)]=\lim _{x \rightarrow a} f(x)+\lim _{x \rightarrow a} g(x)$$

Аналогично предел разности двух функций равен разности пределов этих функций.

Расширенное свойство предела суммы:

Предел суммы нескольких функций равен сумме пределов этих функций:

$$\lim _{x \rightarrow a}\left[f_{1}(x)+\ldots+f_{n}(x)\right]=\lim _{x \rightarrow a} f_{1}(x)+\ldots+\lim _{x \rightarrow 0} f_{n}(x)$$

Аналогично предел разности нескольких функций равен разности пределов этих функций.

3) Предел произведения функции на постоянную величину

Постоянный коэффициэнт можно выносить за знак предела:

$$\lim _{x \rightarrow a} k f(x)=k \lim _{x \rightarrow a} f(x)$$

4) Предел произведения

Предел произведения двух функций равен произведению пределов этих функций:

$$\lim _{x \rightarrow 0}[f(x) g(x)]=\lim _{x \rightarrow 0} f(x) \cdot \lim _{x \rightarrow 2} g(x)$$

Расширенное свойство предела произведения

Предел произведения нескольких функций равен произведению пределов этих функций:

$$\lim _{x \rightarrow a}\left[f_{1}(x) f_{2}(x) \ldots f_{n}(x)\right]=\lim _{x \rightarrow a} f_{1}(x) \cdot \lim _{x \rightarrow 0} f_{2}(x) \cdot \ldots \cdot \lim _{x \rightarrow 2} f_{n}(x)$$

5) Предел частного

Предел частного двух функций равен отношению пределов этих функций при условии, что предел знаменателя не равен нулю:

$$\lim _{x \rightarrow a} \frac{f(x)}{g(x)}=\frac{\lim _{x \rightarrow \infty} f(x)}{\lim _{x \rightarrow 0} g(x)}, \quad$ ecл $\lim _{x \rightarrow a} g(x) \neq 0$$