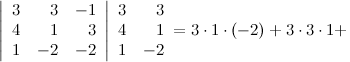Задание. Вычислить определитель
$\Delta=\left| \begin{array}{rrrr}{-2} & {1} & {3} & {2} \\ {3} & {0} & {-1} & {2} \\ {-5} & {2} & {3} & {0} \\ {4} & {-1} & {2} & {-3}\end{array}\right|$ приведением его к треугольному виду.
Решение. Сначала делаем нули в первом столбце под главной диагональю. Все преобразования
будет выполнять проще, если элемент $a_{11}$ будет
равен 1. Для этого мы поменяем местами первый и второй столбцы определителя, что, согласно свойствам определителя,
приведет к тому, что он сменит знак на противоположный:
$$\Delta=\left| \begin{array}{rrrr}{-2} & {1} & {3} & {2} \\ {3} & {0} & {-1} & {2} \\ {-5} & {2} & {3} & {0} \\ {4} & {-1} & {2} & {-3}\end{array}\right|=-\left| \begin{array}{rrrr}{1} & {-2} & {3} & {2} \\ {0} & {3} & {-1} & {2} \\ {2} & {-5} & {3} & {0} \\ {-1} & {4} & {2} & {-3}\end{array}\right|$$
Далее получим нули в первом столбце, кроме элемента $a_{11}$ ,
для этого из третьей строки вычтем две первых, а к четвертой строке прибавим первую, будем иметь:
$$\Delta=-\left| \begin{array}{rrrr}{1} & {-2} & {3} & {2} \\ {0} & {3} & {-1} & {2} \\ {0} & {-1} & {-3} & {-4} \\ {0} & {2} & {5} & {-1}\end{array}\right|$$
Далее получаем нули во втором столбце на месте элементов, стоящих под главной диагональю. И снова, если
диагональный элемент будет равен $\pm 1$ , то
вычисления будут более простыми. Для этого меняем местами вторую и третью строки (и при этом меняется на
противоположный знак определителя):
$$\Delta=\left| \begin{array}{rrrr}{1} & {-2} & {3} & {2} \\ {0} & {-1} & {-3} & {-4} \\ {0} & {3} & {-1} & {2} \\ {0} & {2} & {5} & {-1}\end{array}\right|$$
Далее делаем нули во втором столбце под главной диагональю, для этого поступаем следующим образом:
к третьей строке прибавляем три вторых, а к четвертой - две вторых строки, получаем:
$$\Delta=\left| \begin{array}{rrrr}{1} & {-2} & {3} & {2} \\ {0} & {-1} & {-3} & {-4} \\ {0} & {0} & {-10} & {-10} \\ {0} & {0} & {-1} & {-9}\end{array}\right|$$
Далее из третьей строки выносим (-10) за определитель и делаем нули в третьем столбце под
главной диагональю, а для этого к последней строке прибавляем третью:
$$\Delta=-10 \left| \begin{array}{rrrr}{1} & {-2} & {3} & {2} \\ {0} & {-1} & {-3} & {-4} \\ {0} & {0} & {1} & {1} \\ {0} & {0} & {-1} & {-9}\end{array}\right|=$$
$$=-10 \cdot \left| \begin{array}{cccc}{1} & {-2} & {3} & {2} \\ {0} & {-1} & {-3} & {-4} \\ {0} & {0} & {1} & {1} \\ {0} & {0} & {0} & {-8}\end{array}\right|=(-10) \cdot 1 \cdot(-1) \cdot 1 \cdot(-8)=-80$$
Ответ. $\Delta=-80$
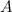 второго порядка, надо от произведения
второго порядка, надо от произведения