Высотой треугольника называется перпендикуляр, опущенный из вершины треугольника на прямую, которая содержит его противоположную сторону.
Содержание:
Определение высоты треугольника
Определение
Каждый треугольник имеет три высоты. Высоту, проведенную из вершины $A$ на сторону $a$, принято обозначать $h_{a}$. Высоты треугольников или их продолжение пересекается в одной точке. В остроугольном треугольнике точка $O$ пересечения высот находится внутри треугольника; в прямоугольном - в вершине прямого угла (совпадает с точкой $C$); в тупоугольном треугольнике - за пределами треугольника. Точка пересечения высот или их продолжений называется ортоцентром.
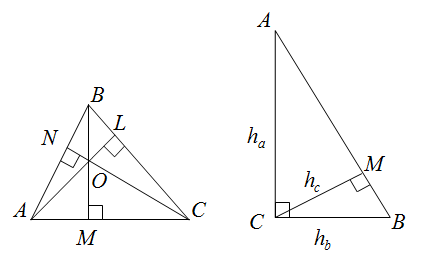
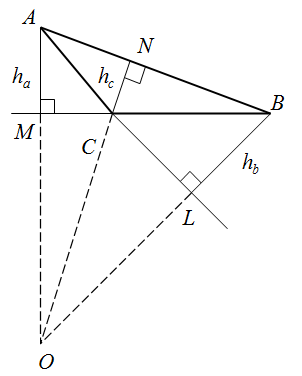
Любую высоту можно найти из соотношений:
$$h_{a}=c \cdot \sin \beta$$
$$h_{a}=\frac{2 S}{a}$$
Примеры решения задач
Пример
Задание. В треугольнике $\Delta A B C$ сторона $A B=2 \sqrt{2}$ мм, $\angle B=45^{\circ}$. Найти высоту, опущенную на сторону $B C$.
Решение. Обозначим искомую высоту $AH$.
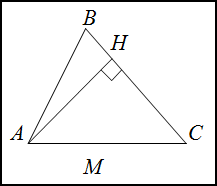
Для нахождения высоты $AH$ воспользуемся формулой
$$h_{a}=c \cdot \sin \beta$$
которая в наших обозначениях запишется следующим образом:
$$A H=A B \cdot \sin \angle B$$
Подставим в последнее равенство исходные данные, получим
$$A H=2 \sqrt{2} \cdot \sin 45^{\circ}$$
$A H=2 \sqrt{2} \cdot \frac{\sqrt{2}}{2}$
$A H=2$ (мм)
Ответ. $A H=2$ мм
Пример
Задание. Одна из сторон треугольника равна 6 см. Найти высоту, опущенную к этой стороне, если площадь треугольника равна 30 см2.
Решение. Для нахождения высоты треугольника, воспользуемся формулой
$$h_{a}=\frac{2 S}{a}$$
Подставим в неё исходные данные
$h_{a}=\frac{2 \cdot 30}{6}$
$h_{a}=10$ (см)
Ответ. $h_{a}=10$ см
Читать дальше: что такое биссектриса треугольника.










