Трапеция - это четырехугольник $A B C D$, две стороны которого параллельны, а две другие не параллельны (рис. 1).
Содержание:
- Определение трапеции
- Свойство трапеции
- Свойства равнобокой трапеции
- Признаки равнобокой трапеции
- Примеры решения задач
Определение трапеции
Определение
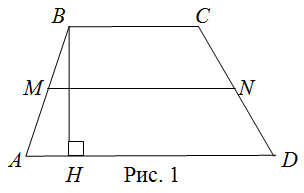
Параллельные стороны трапеции ( $B C$ и $A D$ ) называются основаниями трапеции, а не параллельные ( $A B$ и $C D$ ) - боковыми сторонами. Перпендикуляр ( $B H$ ), проведенный из любой точки одного основание к другому основанию или его продолжению называется высотой трапеции.
Свойство трапеции
Сумма углов прилежащих, прилежащих к боковой стороне равна $180^{\circ}$:
$\angle A+\angle B=180^{\circ}, \angle C+\angle D=180^{\circ}$ (рис 1)
Отрезок, соединяющий середины боковых сторон трапеции, называется средней линией трапеции. Средняя линия трапеции параллельна основаниям и равна их полусумме:
$$M N=\frac{A D+B C}{2}$$
Среди всех трапеций можно выбрать два особых класса трапеций: прямоугольные и равнобокие трапеции.
Определение
Прямоугольной называется трапеция, у которой один из углов прямой.
Равнобокой называется трапеция, у которой боковые стороны равны.
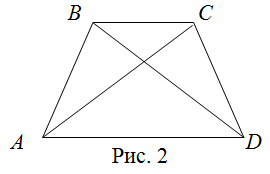
Свойства равнобокой трапеции
- В равнобокой трапеции углы при основании попарно равны $\angle A=\angle D, \angle B=\angle C$.
- Диагонали равнобокой трапеции равны $A C=B D$.
Признаки равнобокой трапеции
- Если углы при основании трапеции равны, то трапеция равнобокая.
- Если в трапеции диагонали равны, то она равнобокая.
Площадь трапеции:
$$S=\frac{a+b}{2} \cdot h$$
где $a$ и $b$ - основания трапеции, а $h$ - ее высота.
Примеры решения задач
Пример
Задание. Высота равнобокой трапеции, проведенная из тупого угла, делит основание на отрезки длиной 5 см и 11 см. Найти периметр трапеции, если её высота равна 12 см.
Решение. Сделаем рисунок (рис. 3)
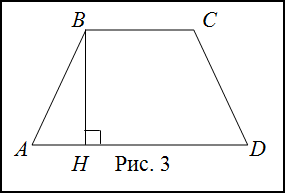
$ABCD$ - равнобокая трапеция, $BH$ - высота, $BH = 12$ см, $AH = 5$ см, $HD = 11$ см.
Рассмотрим $\Delta A B H$, он прямоугольный ( $\angle H=90^{\circ}$ ). По теореме Пифагора
$$A B=\sqrt{B H^{2}+A H^{2}}$$
подставляя исходные данные, получим
$A B=\sqrt{12^{2}+5^{2}}$
$A B=\sqrt{144+25}=\sqrt{169} \Rightarrow A B=13$ (см)
Так как трапеция $A B C D$ равнобокая, то её боковые стороны равны: $A B=C D=13$ см. Большее основание трапеции равно: $A D=A H+H D$, $A D=5+11=16$ (см). Меньшее основание трапеции будет равно: $B C=A D-2 A H, B C=16-2 \cdot 5=6$ (см). Периметр трапеции равен:
$P_{A B C D}=A B+B C+C D+A D$
$P_{A B C D}=13+6+13+16$
$P_{A B C D}=48$ (см)
Ответ. $P_{A B C D}=48$ см
Пример
Задание. В прямоугольной трапеции две меньшие стороны равны 2 дм, а один из углов $45^{\circ}$. Найти площадь трапеции.
Решение. Сделаем рисунок (рис. 4)
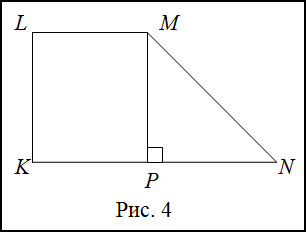
$K L M N$ - прямоугольная трапеция, $K L=L M=2$ дм, $L K \perp K N$, $\angle M L K=45^{\circ}$. Из вершины $M$ опустим высоту $MP$ на основание $KN$. Рассмотрим $\Delta M N P$, он прямоугольный ( $\angle M P N=90^{\circ}$ ). Так как $\angle M L K=45^{\circ}$, то
$\angle N M P=180^{\circ}-\angle M P N-\angle M L K$
$\angle N M P=180^{\circ}-90^{\circ}-45^{\circ}=45^{\circ}$
Таким образом, $\angle M L K=\angle N M P$ и $\Delta M N P$ еще и равнобедренный. Следовательно, $M P=P N$. Так как $L K=M P=2$ дм, следовательно и $P N=2$ дм. Большее основание $K N=K P+P N$, так как $L M=K P$, получим $K N=2+2=4$ (дм).
Площадь трапеции вычислим по формуле:
$$S=\frac{a+b}{2} \cdot h$$
, в нашем случае она примет вид:
$$S_{K L M N}=\frac{L M+K N}{2} \cdot M P$$
Подставляя известные значения, получим
$S_{K L M N}=\frac{2+4}{2} \cdot 2=6$ (дм2)
Ответ. $S_{K L M N}=6$ дм2
Читать дальше: что такое треугольник.










