Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
Содержание:
Формула теоремы косинусов
Теорема
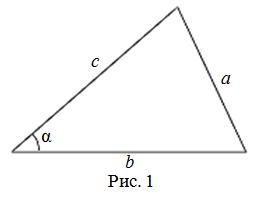
То есть для плоского треугольника (рис. 1) со сторонами $a$, $b$ и $c$ и углом $\alpha$, противолежащим стороне $a$, справедливо соотношение:
$a^{2}=b^{2}+c^{2}-2 b c \cos \alpha$
Теорема косинусов является обобщением теоремы Пифагора. Утверждения, обобщающие теорему Пифагора и эквивалентные теореме косинусов, были сформулированы отдельно для случаев острого и тупого угла в 12 и 13 предложениях II книги "Начал" древнегреческого математика Евклида (ок. 300 г. до н. э.). Утверждения, эквивалентные теореме косинусов для сферического треугольника, применялись в сочинениях математиков стран Средней Азии. Теорему косинусов для сферического треугольника в привычном нам виде сформулировал выдающийся немецкий астролог, астроном и математик Региомонтан (1436 - 1476), назвав её "теоремой Альбатегния" (по имени выдающегося средневекового астронома и математика Абу Абдаллах Мухаммад ибн Джабир ибн Синан ал-Баттани (858 - 929).
В Европе теорему косинусов популяризовал французский математик Франсуа Виет (1540 - 1603) в 16 столетии. В начале 19 века её стали записывать в принятых по сей день алгебраических обозначениях.
Следствие из теоремы косинусов
-
Теорема косинусов может быть использована для нахождения косинуса угла треугольника (рис. 1):
$$\cos \alpha=\frac{b^{2}+c^{2}-a^{2}}{2 b c}$$
-
Если $b^{2}+c^{2}-a^{2}>0$, то угол $\alpha$ - острый;
Если $b^{2}+c^{2}-a^{2}=0$, то угол $\alpha$ - прямой;
Если $b^{2}+c^{2}-a^{2} \lt 0$, то угол $\alpha$ - тупой.
Примеры решения задач
Пример
Задание. В треугольнике $ABC AC=3, BC=5$ и $AB = 6 .$ Найти угол, противолежащий стороне $AB$
Решение. Согласно следствию из теоремы косинусов, имеем:
$$\cos \angle A C B=\frac{A C^{2}+B C^{2}-A B^{2}}{2 \cdot A C \cdot B C}=\frac{3^{2}+5^{2}-6^{2}}{2 \cdot 3 \cdot 5}=$$
$$=\frac{9+25-36}{30}=-\frac{2}{30}=-\frac{1}{15}$$
Тогда
$$\angle A C B=\arccos \left(-\frac{1}{15}\right)$$
Ответ. $\angle A C B=\arccos \left(-\frac{1}{15}\right)$
Пример
Задание. Задан треугольник $ABC$, длины сторон которого $AC=17, BC=14, \angle ACB=60^{\circ}$. Найти длину третьей стороны рассматриваемого треугольника.
Решение. Согласно теореме косинусов
$$A B^{2}=A C^{2}+B C^{2}-2 \cdot A C \cdot B C \cdot \cos \angle A C B=$$
$$=17^{2}+14^{2}-2 \cdot 17 \cdot 14 \cdot \cos 60^{\circ}=289+196-238=24$$
Тогда
$$A B=\sqrt{247}$$
Ответ. $A B=\sqrt{247}$










