Содержание:

Формулировка теоремы Фалеса

Теорема

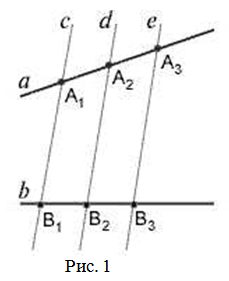
Если на одной из двух прямых отложить последовательно несколько отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой пропорциональные отрезки (рис. 1).

В теореме нет ограничений на взаимное расположение секущих (она верна как для пересекающихся прямых, так и для параллельных). Также не важно, где находятся отрезки на секущих.

Теорема

Обобщённая теорема Фалеса

Параллельные прямые отсекают на секущих пропорциональные отрезки (рис. 1):

$$\frac{A_{1} A_{2}}{B_{1} B_{2}}=\frac{A_{2} A_{3}}{B_{2} B_{3}}=\frac{A_{1} A_{3}}{B_{1} B_{3}}$$

Теорема Фалеса является частным случаем обобщённой теоремы Фалеса, поскольку равные отрезки можно считать пропорциональными отрезками с коэффициентом пропорциональности, равным 1.

Теорема

Обратная теорема Фалеса

Если прямые, пересекающие две другие прямые (параллельные или нет), отсекают на обеих из них равные (или пропорциональные) между собой отрезки, начиная от вершины, то такие прямые параллельны (рис. 2).

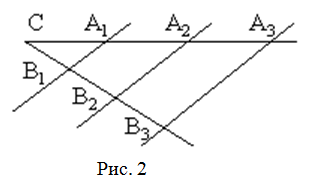
Замечание. В обратной теореме Фалеса важно, что равные отрезки начинаются от вершины.

Примеры решения задач

Пример

Задание. Разделить данный отрезок на четыре равные части.

Решение. Пусть $AB$ - заданный отрезок (рис. 3), который необходимо разделить на четыре равные части.

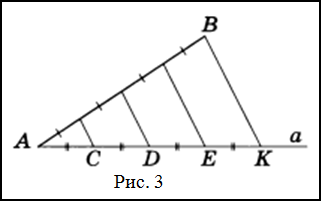
Через точку $A$ проведем произвольную полупрямую $a$ и отложим на ней последовательно четыре равных между собой отрезка $AC, CD, DE, EK$ .

Соединим точки $B$ и $K$ отрезком и проведем через оставшиеся точки $C$, $D$ и $E$ прямые, параллельные прямой $BK$ так, чтобы они пересекли отрезок $AB$ .

Согласно теореме Фалеса отрезок $AB$ разделится на четыре равные части.


Warning: file_put_contents(./students_count.txt): failed to open stream: Permission denied in /var/www/webmath-q2ws/data/www/webmath.ru/poleznoe/guide_content_banner.php on line 20
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 472 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. На стороне $AB$ треугольника $ABC$ отмечена точка $K$. Отрезок $CK$ пересекает медиану $AM$ треугольника в точке $P$, причем $AK = AP$. Найти отношение $BK : PM$ .

Решение. Проведем через точку $M$ прямую, параллельную $CK$, которая пересечет $AB$ в точке $D$ (рис. 4).

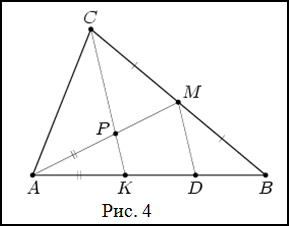
По теореме Фалеса $BD = KD$ .

По теореме о пропорциональных отрезках имеем, что

$$P M=K D=\frac{B K}{2} \Rightarrow B K: P M=2: 1$$

Ответ. $B K: P M=2: 1$

Историческая справка

Теорема Фалеса (а также теоремы Чевы и Менелая) применяются в первую очередь тогда, когда в задаче даны соотношения между отрезками. Очень часто при этом приходится проводить дополнительный отрезок.

Аргентинская музыкальная группа представила песню, посвящённую теореме. В видеоклипе для этой песни приводится доказательство для прямой теоремы для пропорциональных отрезков.

Теорема Фалеса до сих пор используется в морской навигации в качестве правила о том, что столкновение судов, двигающихся с постоянной скоростью, неизбежно, если сохраняется курс судов друг на друга.

Вне русскоязычной литературы теоремой Фалеса иногда называют другую теорему планиметрии, а именно, утверждение о том, что вписанный угол, опирающийся на диаметр окружности, является прямым. Открытие этой теоремы действительно приписывается Фалесу, о чём есть свидетельство Прокла.