Стороны треугольника пропорциональны синусам противолежащих углов.
Содержание:
Формулировка теоремы синусов
Теорема
$\frac{a}{\sin \alpha}=\frac{b}{\sin \beta}=\frac{c}{\sin \gamma}$
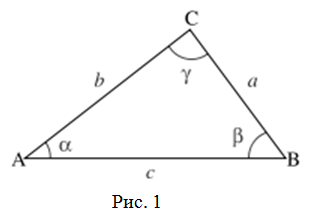
Теорема синусов устанавливает зависимость между сторонами треугольника и противолежащими им углами.
Расширенная теорема синусов
Теорема
Для произвольного треугольника имеет место соотношение:
$\frac{a}{\sin \alpha}=\frac{b}{\sin \beta}=\frac{c}{\sin \gamma}=2 R$
Здесь $R$ - радиус окружности, описанной около рассматриваемого треугольника.
Примеры решения задач
Пример
Задание. Основание треугольника равно 10 см, один из углов при основании равен $45^{\circ}$, а противолежащий основанию угол равен $60^{\circ}$. Найдите сторону, противолежащую углу в $45^{\circ}$.
Решение. Пусть искомая сторона - $x$ см. Тогда по теореме синусов имеем:
$$\frac{10}{\sin 60^{\circ}}=\frac{x}{\sin 45^{\circ}} \Rightarrow x=\frac{10 \cdot \frac{\sqrt{2}}{2}}{\frac{\sqrt{3}}{2}}=\frac{10 \sqrt{2}}{\sqrt{3}}=\frac{10 \sqrt{6}}{3} (\mathrm{см})$$
Ответ.$\frac{10 \sqrt{6}}{3}(\mathrm{см})$
Пример
Задание. В треугольнике $A B C \quad \angle A=45^{\circ}, \angle C=15^{\circ},$
$B C=4 \sqrt{6}$. Найти $A C$ .
Решение. Согласно теореме о сумме углов треугольника
$$\angle A+\angle B+\angle C=180^{\circ} \Rightarrow \angle B=180^{\circ}-45^{\circ}-15^{\circ}=$$
Сторону $AC$ найдем по теореме синусов:
$$\frac{A C}{\sin \angle B}=\frac{B C}{\sin \angle A} \Rightarrow \frac{A C}{\sin \angle 120^{\circ}}=\frac{4 \sqrt{6}}{\sin \angle 45^{\circ}} \Rightarrow$$
$$\Rightarrow \frac{A C}{\frac{\sqrt{3}}{2}}=\frac{4 \sqrt{6}}{\frac{\sqrt{2}}{2}} \Rightarrow A C=\frac{4 \sqrt{18}}{\sqrt{2}}=4 \cdot \sqrt{9}=12$$
Ответ. $A C=12$
Историческая справка
Самое древнее доказательство для теоремы синусов на плоскости описано в книге "Трактат о полном четырёхстороннике" персидского математика, механика и астронома Насира ад-Дина Ат-Туси (1201 - 1274), которая была написана в 13 веке. Теорема синусов для сферического треугольника была доказана математиками средневекового Востока ещё в 10 веке. В труде западноарабского математика, астронома и законоведа Ал-Джайяни (989 - 1050) 11 века "Книга о неизвестных дугах сферы" приводилось общее доказательство теоремы синусов на сфере.










