Содержание:

Определение суммы чисел

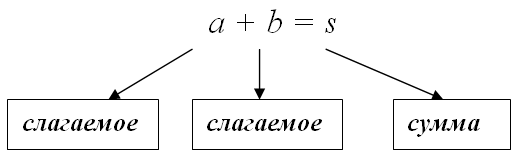
Суммой $s$ (лат. summa - итог, общее количество) чисел $a_{1}, a_{2}, \dots, a_{n}$ называется результат суммирования этих чисел: $s=a_{1}+a_{2}+\ldots+a_{n}$ . В частности, если складывается два числа $a$ и $b$, то

Пример

Задание. Найти сумму чисел:

1)  $12$  и $15$      2)  $1,1 ; 2,2 ; 3,3$  и $4,4$ 

Ответ.

$12+15=27$

$1,1+2,2+3,3+4,4=11$

Свойства суммы чисел

  1. Коммутативность: $n+m=m+n$

  2. Ассоциативность: $(n+m)+k=n+(m+k)$

    На основании этих свойств можем заключить, что от перестановки мест слагаемых сумма не изменяется.

  3. Дистрибутивность по отношению к умножению

    $$(n+m) \cdot k=n \cdot k+m \cdot k$$


Warning: file_put_contents(./students_count.txt): failed to open stream: Permission denied in /var/www/webmath-q2ws/data/www/webmath.ru/poleznoe/guide_content_banner.php on line 20
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 462 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Найти сумму чисел удобным способом:

1)  $15+17+13$   ;   2)  $34+22+16+18$ 

Решение. По свойствам сложения имеем

$$15+17+13 =15+(17+13)=15+30=45 $$

$$34+22+16+18 =(34+16)+(22+18)=50+40=90 $$

Ответ. 1)  $15+17+13=45$

            2)  $34+22+16+18=90$

При сложении больших чисел или десятичных дробей используется сложение в столбик.

Пример

Задание. Найти сумму чисел удобным способом:

1)  $1562+13827$   ;   2)  $34,71+356,161$ 

Решение. Складываем эти числа в столбик, для этого запишем их друг под другом, разряд под разрядом. В случае десятичных дробей ориентируемся на то, чтобы запятая первого числа стояла под запятой второго. Далее складываем числа стоящие друг под другом, двигаясь справа на лево и записывая результата под чертой дроби. Если сумма чисел в одном столбце превышает десять, то количество десятков прибавляем к числам стоящим в следующем столбце слева от этого столбца:

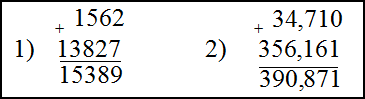
Ответ. 1)  $1562+13827=15389$

            2)  $34,71+356,161=390,871$

Сложение рациональных дробей производится по правилу

$$\frac{m}{n}+\frac{p}{q}=\frac{m \cdot q+n \cdot p}{n \cdot q}$$

Пример

Задание. Найти сумму чисел:

1)  $\frac{1}{4}+\frac{1}{6}$   ;   2)  $\frac{2}{3}+1 \frac{1}{2}$ 

Решение. Вычислим первую сумму используя правило сложения рациональных чисел

$$\frac{1}{4}+\frac{1}{6}=\frac{1 \cdot 6+1 \cdot 4}{4 \cdot 6}=\frac{6+4}{24}=\frac{10}{24}$$

Числитель и знаменатель полученной дроби можно сократить на 2, тогда в ответе получим

$$\frac{1}{4}+\frac{1}{6}=\frac{5}{12}$$

Для вычисления второй суммы, преобразуем сначала второе слагаемое в неправильную дробь, для этого умножим целую часть на знаменатель и прибавим полученное число к числителю. Далее применим правило сложение рациональных дробей

$$\frac{2}{3}+1 \frac{1}{2}=\frac{2}{3}+\frac{3}{2}=\frac{2 \cdot 2+3 \cdot 3}{3 \cdot 2}=\frac{4+9}{6}=\frac{13}{6}$$

Выделим в полученной дроби целую часть, для этого разделим числитель на знаменатель с остатком. Полученное частное запишем в целую часть, а остаток от деления в числитель.

$$\frac{2}{3}+1 \frac{1}{2}=2 \frac{1}{6}$$

Ответ. 1)  $\frac{1}{4}+\frac{1}{6}=\frac{5}{12}$   ;    2)  $\frac{2}{3}+1 \frac{1}{2}=2 \frac{1}{6}$ 

Больше примеров решений Операции с дробями онлайн

Читать дальше: что такое произведение чисел.